Copyright Notice
Copyright 1998-2024 Takashi Tanaka
This software is free for use, however, the author retains the copyright to this software. It may be distributed in its entirety only and may not be included in any other product or be distributed as part of any commercial software.
This software is distributed with NO WARRANTY OF ANY KIND. Use at your own risk. The author is not responsible for any damage done by using this software and no compensation is made for it.
This software has been developed, improved and maintained as voluntary work of the author. Even if problems and bugs are found, the author is not responsible for improvement of them or version up of the software.
If you are submitting articles to scientific journals with the results obtained by using this software, please cite the relevant references. For details, refer to Introduction.
Introduction
This document describes the instruction to use the free software SPECTRA, a synchrotron radiation (SR) calculation code, and is located in "[SPECTRA Home]/help", where "[SPECTRA Home]" is the directory where SPECTRA has been installed. Brief explanations on the software and numerical implementation of SR calculation are given here, together with a simple instruction of how to get started. Note that "MathJax" javascript library is needed to correctly display the mathematical formulas, which is available online. If you need to read this document offline, "MathJax" should be installed in "[SPECTRA Home]/help" directory.
Overview
SPECTRA is a computer program to numerically evaluate the characteristics of radiation emitted from various synchrotron radiation (SR) sources, such as bending magnets and insertion devices (IDs, i.e., wigglers and undulators). In addition, SR sources with arbitrary magnetic fields are available by importing the magnetic field data prepared by the user. This makes it possible to estimate the real performance of the SR source by using the magnetic field distribution actually measured by field measurement instruments such as Hall probes.
To compute the characteristics of radiation and evaluate the performances of SR sources, a large number of parameters are required to specify the electron beam, light source, observation conditions, and options for numerical operations. SPECTRA is equipped with a fully graphical user interface (GUI) which facilitates configurations of them. In addition, a post-processor is included to verify the computation results graphically. Since version 11.0, the GUI is written based on the web technologies, i.e., HTML, CSS and Javascript, with the assistance of "node.js" and "tauri" to build a standalone application. For visualization of calculation results and imported data, "Plotly" library is used. Thanks to portability of these libraries, SPECTRA will run on most of the platforms such as Microsoft Windows, Macintosh OS X and Linux. SPECTRA does not require any other commercial software or libraries.
The numerical part of SPECTRA ("solver") is written in C++11 with the standard template library (STL). For bending magnets, wigglers and undulators, numerical implementation is based on the well-known expressions on SR, and the so-called far-field approximation is available for fast computation. For more accurate evaluation, expressions on SR in the near-field region are used for numerical computation. In this case, characteristics of SR emitted from both the ideal- and arbitrary-field devices can be calculated. For details of numerical implementation, refer to [1] and [2]. The users who are publishing their results obtained with SPECTRA are kindly requested to cite [3].
Before ver. 7.2, the magnetic field was assumed to be constant in the transverse (x-y) plane. In other words, only the dipole components were taken into account. This considerably simplifies the numerical algorithm not only in the trajectory calculation but also in the spatial integration to take into account the finite electron beam emittance. In ver. 8.0, an arbitrary magnetic field has been supported to enable the evaluation of the effects due to quadrupole magnets between undulator segments and the undulator natural focusing, which would be significant for low-energy electrons. In ver. 9.0, an arbitrary electron bunch profile has been supported. The user can specify the longitudinal bunch profile, or import the macroparticle coordinates in the 6D phase space, which is usually created by the start-to-end simulation for accelerators.
In ver. 10.0, a new function to compute the photon flux density in the 4D phase space (x,x',y,y') has been implemented[4], which enables the rigorous estimation of the brilliance (brightness) of typical SR sources and the photon distribution at the source point to be utilized in other computer codes for ray-tracing simulations. Based on the phase-space density computed with this function, a numerical scheme to decompose the partially-coherent radiation into a number of coherent modes (coherent mode decomposition: CMD)[5] has been later implemented in version 10.1, which is explained in more detail here. The users who are publishing their results obtained using these numerical schemes are kindly requested to cite the relevant references. Also implemented in ver. 10.1 is a function to compute the surface power density, which is convenient to compute the heat load on the inner wall of a vacuum chamber located near the SR source and exposed to SR with a shallow incident angle.
In ver. 11.0, the solver has been widely revised to be consistent with the C++11 standard and to facilitate the maintenance and bug fix. A new function has been also implemented to compute the volume power density; this is to evaluate the heat load of SR incident on an object, which gradually decays while it transmits the object. The output data will probably be used later for heat analysis of high heat-load components in the SR beamline based on the finite element method. In addition to the above revisions, two important upgrades have been made in ver. 11. First, the format of the input parameter file has been changed from the original one (and thus not readable in other applications) to JSON (JavaScript Object Notation) format. Because the output data is also given by a JSON file, it is now easy to communicate with other 3rd-party applications. Second, the framework (GUI library) has been switched to those based on web technologies (HTML, CSS, and JavaScript). This enhances the portability between different platforms (operating systems).
In ver. 12.0, the python support, which was experimentally implemented in ver 11.0, has been extensively enhanced. Python package as a user interface to communicate with the SPECTRA GUI has been developed and is available from the Python Package Index repository (by a normal pip command). Note that this function is based on "Selenium" framework that is usually used to automatically operate the web browser. For details about how it works, refer to Python User Interface
Following the enhancement of the python support deseribed abvove, an imporant decision has been made in ver. 12.0 regarding the support for Linux platforms; because of the too diverse versions of relevant (not only GUI but also core) libraries, it is almost impossible to prepare the conventional desktop application to support all the potential distributions. Thus, only one package compiled on Ubuntu 20.04, which can be installed through dpkg/apt, is prepared as of May 2024. The users of other Linux distributions are kindly recommended to try the python version.
Getting Started
- Open a parameter file by running [File]-[Open a Parameter File] command, or run [File]-[Create a New Parameter File] command to start with a new parameter set.
- Select the calculation type from submenus in [Select Calculation].
- Edit the parameters if necessary and specify the directory and data name to save the calculation results.
- Run [Run]-[Start Calculation] command to start a calculation with current parameters.
- A "Progressbar" appears to inform the calculation status.
- To verify the calculation results after completion of the calculation, click "Post-Processing" tab, select the name of the output file and item(s) to check for visualization. Refer to Post-Processing for details.
Operation of the GUI
SPECTRA GUI is composed of three tabbed panels entitled as "Main Parameters", "Pre-Processing", and "Post-Processing", which are explained in what follows.
Main Parameters
The "Main Parameters" tabbed panel is composed of a number of subpanels entitled as "Accelerator", "Light Source", "Configurations", "Output File", and "Calculation Status/Processes". Note that the "Accelerator", "Light Source""Output File" subpanels are always displayed, while the others are shown when necessary.
Accelerator Subpanel
Display and edit the parameters and numerical conditions related to the electron beam. For details, refer to Accelerator Parameter List.
Light Source Subpanel
Display and edit the parameters and numerical conditions related to the light source. For details, refer to Light Source Parameter List.
Configurations Subpanel
Display and edit the parameters and numerical conditions related to the observation of radiation. For details, refer to Configurations Parameter List.
Output File Subpanel
Specify the path, name and format of the output file.
| Parameter/Option | Detail |
| Format | Select the format of the output file from three options: "JSON" for the JSON format, "ASCII" for the ASCII (simple text with the suffix ".txt") format, and "Both" for the both options. Note that the ASCII format is identical to that in the older (&lE 10.2) versions, however, it cannot be used later for Post-Processing (visualization of the data). |
| Folder | Input the path of the output file in [Folder], a prefix text in [Prefix], and a serial number in [Serial Number]. Then the output file name is given as [Folder]/[Prefix]-[Serial Number].[Format], like "/Users/data/test-1.json", where "/Users/data", "test", 1, and "json" refer to [Folder], [Prefix], [Serial Number] and [Format]. Note that the serial number can be -1 (negative), in which case it is not attached to the data name. |
| Prefix | |
| Serial Number | |
| Comment | Input any comment in [Comment] if necessary, which is saved in the output file and can be referred later on. |
Note that a spread sheet "Output Data" is shown in this subpanel, if "Fixed Point Calculation" is selected as the calculation type. Click "Start Calculation" to start a calculation using current parameters and options, then the results are displayed when it is completed.
Calculation Status/Processes Subpanel
Display the status of a calculation in progress, or the list of Calculation Status/Processes. Click "Cancel" to stop the calculation currently running, "Cancel All" to terminate all the calculations, and "Remove" to remove the selected process.
Pre-Processing
The "Pre-Processing" tabbed panel assists the pre-processing, or the arrangement of numerical conditions not displayed in the "Main Parameters" panel.
Data Import
Import a data set prepared by the user, which is necessary for several types of calculations. The types of data sets available in SPECTRA are summarized below.
| Name in Pre-Processing Subpanel | Details | Dimension | Independent Variable(s) | Items |
| Current Profile | undefined | 1 | time | I |
| E-t Profile | undefined | 2 | time , DE/E | j |
| Field Profile | undefined | 1 | z | Bx , By |
| Field Profile (1 Period) | undefined | 1 | z | Bx , By |
| Gap vs. Field | undefined | 1 | Gap | Bx , By |
| Custom Filter | undefined | 1 | Energy | Transmission |
| Depth-Position Data | undefined | 0 | Depth | |
| Seed Spectrum | undefined | 1 | Wavelength | Intensity, Phase |
Meanings of the items and variables are as follows.
- time: arrival time, or longitudinal position along the electron bunch
- DE/E: normalized energy deviation (dimensionless)
- I: beam current (A)
- j: beam current density (A/100%)
- z: longitudinal coordinate along the beam axis
- Bx,By: horizontal and vertical magnetic fields
- Gap: gap of the ID
- Depth: depth positions where the Volume Power Density is calculated
The unit of j may need to be explained; it is given as the current per unit energy band; in a mathematical form, \[I(t)=\int j\left(t, \frac{DE}{E}\right) d\frac{DE}{E}\]
The format of the ASCII file for the 1D data is as follows (magnetic field distribution as an example)
z Bx By
-8.959978e-01 5.174e-05 7.035e-06
-8.949972e-01 5.423e-05 7.062e-06
-8.939967e-01 5.646e-05 7.244e-06
(omitted)
8.979989e-01 4.801e-05 6.639e-06
8.989994e-01 4.582e-05 6.327e-06
9.000000e-01 4.409e-05 6.456e-06
The 1st line (title) is optional. In the above format, the interval of the independent variable (z) does not have to be necessarily constant, which is not the case for the 2D data; the format should as follows
time DE/E j
-1.0e-3 -0.01 0.001
-0.9e-3 -0.01 0.002
-0.8e-3 -0.01 0.003
(omitted)
0.8e-3 -0.01 0.003
0.9e-3 -0.01 0.002
1.0e-3 -0.01 0.001
-1.0e-3 -0.008 0.001
-0.9e-3 -0.008 0.002
-0.8e-3 -0.008 0.003
(omitted)
0.8e-3 -0.008 0.003
0.9e-3 -0.008 0.002
1.0e-3 -0.008 0.001
(omitted)
-1.0e-3 0.01 0.001
-0.9e-3 0.01 0.002
-0.8e-3 0.01 0.003
(omitted)
0.8e-3 0.01 0.003
0.9e-3 0.01 0.002
1.0e-3 0.01 0.001
For reference, such a data format is created in the C/C++ language as follows.
for(n = 0; n < N; n++){
for(m = 0; m < M; m++){
cout << t[m] << " " << de[n] << " " << j[m][n] << endl;
}
}Note that the order of the "for loop" is arbitrary; the 1st and 2nd lines can be swapped in the above example.
After preparing the ASCII file, click "Import" button and specify the file name in the dialog box to import it. The unit of each item should be chosen before importing, in the Units for Data Import dialog box that pops up by running [Edit]-[Units for Data Import] command or clicking "Edit Units" button. Note that the unit of the imported data cannot be changed, so you need to import the data again with the correct unit in case a wrong unit has been chosen. Also note that the units of several items (I, j, DE/E) are fixed, and cannot be selected when importing.
Visualization
After importing, the data sets can be visualized to verify if the configurations (unit and format of the data file) are correct. An example is shown below.
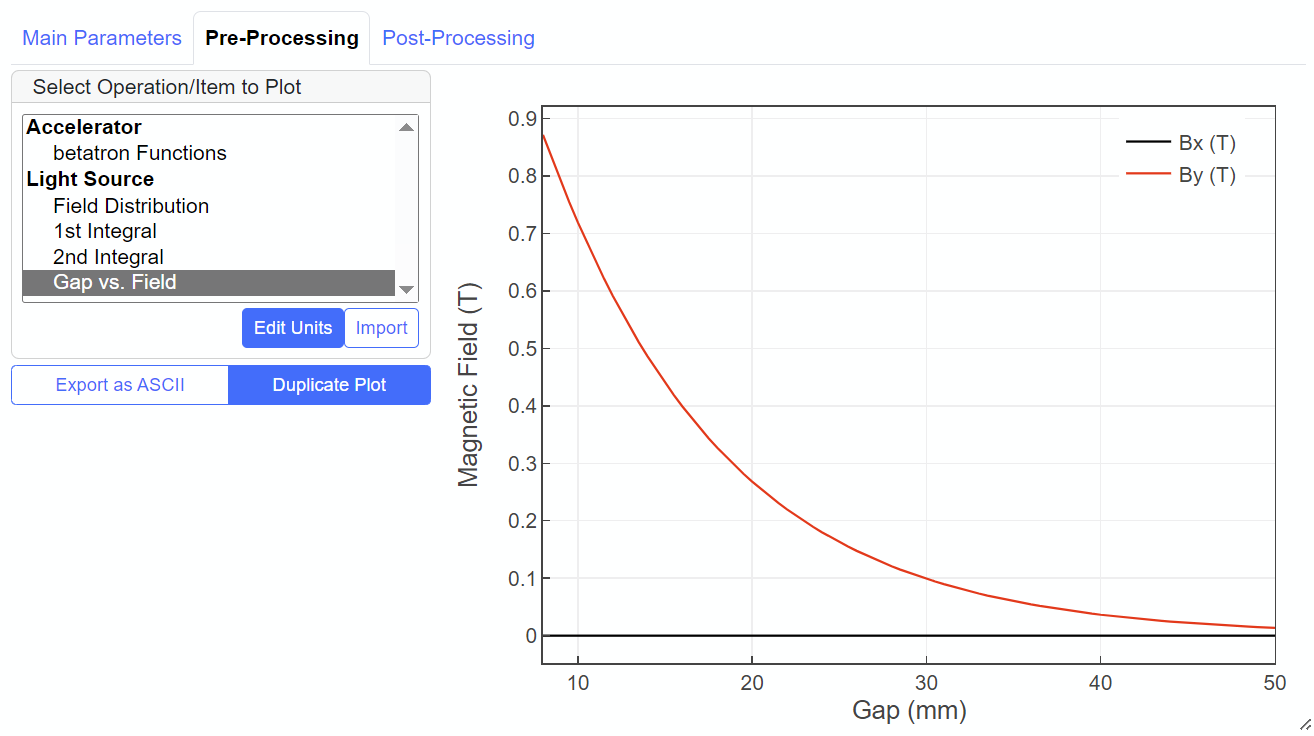
Besides the imported data sets as described above, there exist a number of items that can be visualized, which are listed in the top left of this subpanel. Just click one of them for visualization. Note that several of them are available only under specific conditions, which are summarized below.
| Name in Pre-Processing Subpanel | Details | Availability | |
| Accelerator | betatron Functions | betatron functions within the light source | |
| Light Source | Field Distribution | Magnetic field distribution along the longitudinal axis | |
| 1st Integral | 1st integrals, corresponding to the velocity of an electron | ||
| 2nd Integral | 2nd integrals, corresponding to the electron trajectory | ||
| Phase Error | Phase error [6] evaluated as a function the magnet pole number. Note that the number of end poles (used for the orbit adjustment and should be eliminated for the phase error evaluation) is automatically determined; to be specific, those with the peak field less than 95% of the average are ignored. | "User Defined" sources and/or "Add Phase Error" option | |
| Harmonic Intensity | Reduction of photon intensity at each harmonic due to magnetic errors evaluated by analytical methods. Refer to below for details. | ||
| Filter/Absorber | Transmission Rate | Transmission rate of the filter | "Filtering" options excluding "None" |
| Absorption Rate | Absorption rate of the absorber | "Volume Power Density" calculations | |
Analytical Method to Evaluate the Harmonic Intensity
It is well known that the effects due to magnetic errors in undulators can be evaluated using an analytical formula \[I_r/I_0=\exp(-k^2\sigma_{\phi}^2),\] where $I_0$ means the photon intensity available with an ideal condition, $I_r$ means that in a real condition with magnetic errors, $k$ is the harmonic number, and $\sigma_{\phi}$ is the RMS phase error.
Although the above formula is valid for radiation emitted by a single electron observed on axis (with an infinitely narrow angular acceptance), it overestimates the effects due to magnetic errors in a more realistic condition that the electron beam emittance and energy spread are finite, and/or the the angular acceptance in the beamline is not narrow; these factors effectively work to recover the normalized intensity $I_r/I_0$. To estimate $I_r/I_0$ with these recovery factors, an alternative method [9] can be used, whose results are shown together with those using the conventional method.
Analyze Particle Data
"Analyze Particle Data" pre-processing operation is available when "Particle Distribution" is selected as "Bunch Profile", as shown below. Note that the user needs to specify in advance the data file containing the macroparticle positions in the 6D phase space, which is usually generated by another simulation code. Refer to Particle Distribution for details.
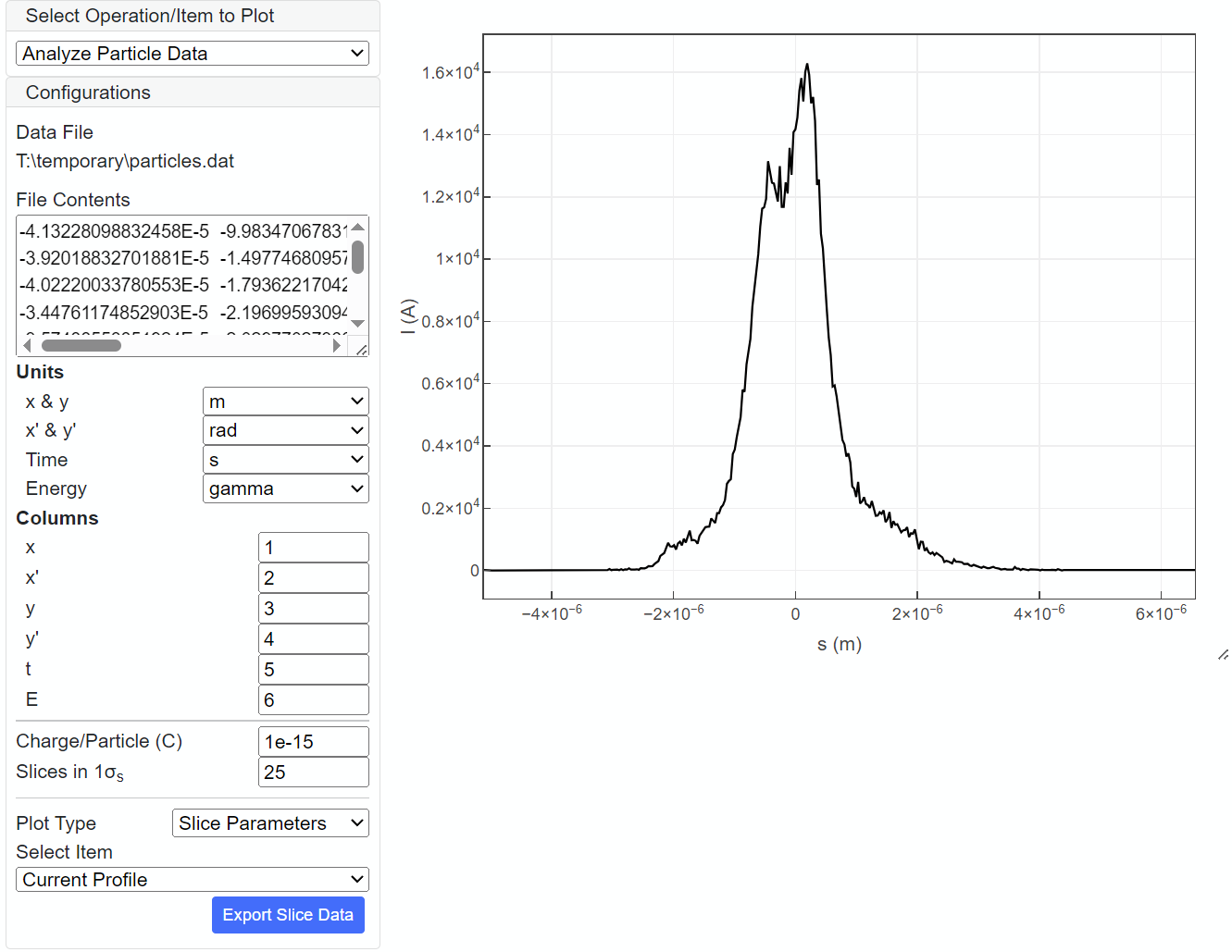
Once "Bunch Profile" is specified, SPECTRA automatically loads the file to analyze the particle data. For convenience, part of the data file is shown in "File Contents" Select the unit and column index for each coordinate variable of the 6D (x,x',y,y',t,E) phase space and input relevant parameters. In the above example, each macroparticle has the charge of 3.5fC with "x" coordinate (horizontal position) located in the 1st column and the unit of m. Note that"Slices in 1σs" specifies the number of bins in the RMS bunch length, to be used for data analysis. Then, additional configurations appear in the GUI to specify how to visualize the results of analysis. In the above example, the current profile is plotted. Upon revision of the configurations above, SIMPLEX automatically analyzes the data with the new configuration and visualizes the result.
Besides the slice parameters shown in the above example, macroparticle distributions can be directly plotted. For example, distribution in the (E-t) phase space is plotted in the figure below.
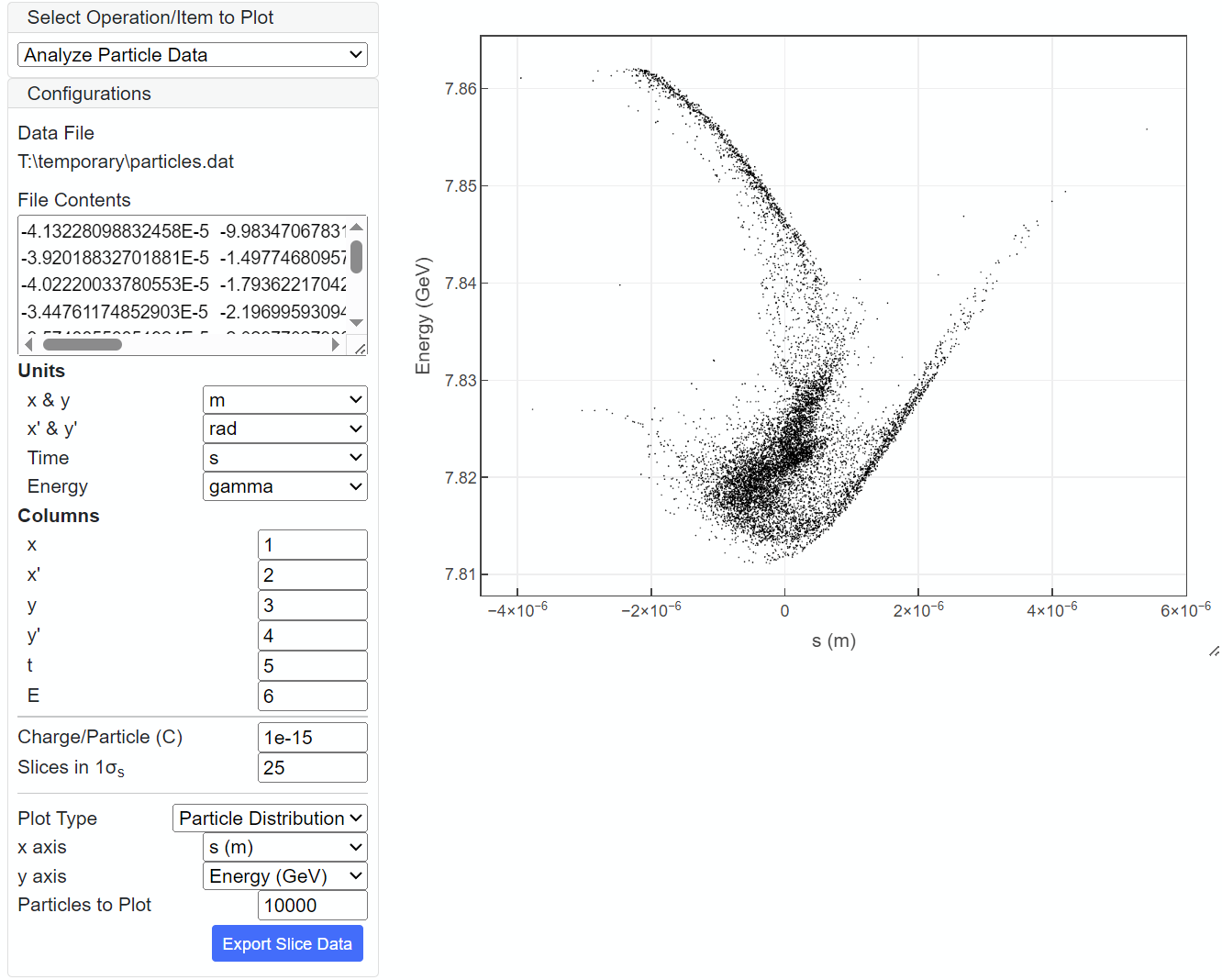
The result of analysis can be exported and saved as an ASCII file; "Export Selected" exports the data currently plotted, while "Export Slice Data" exports the whole slice data (slice paramters vs. s). The exported data file can be used later as the custom data file for slice parameters or current profile.
Post-Processing
The "Post-Processing" tabbed panel assists the user to visualize the calculation results. The output file is automatically loaded upon completion of a calculation, or alternatively, the existing output files can be imported. To do so, click "Import" button and specify the path of the output file.
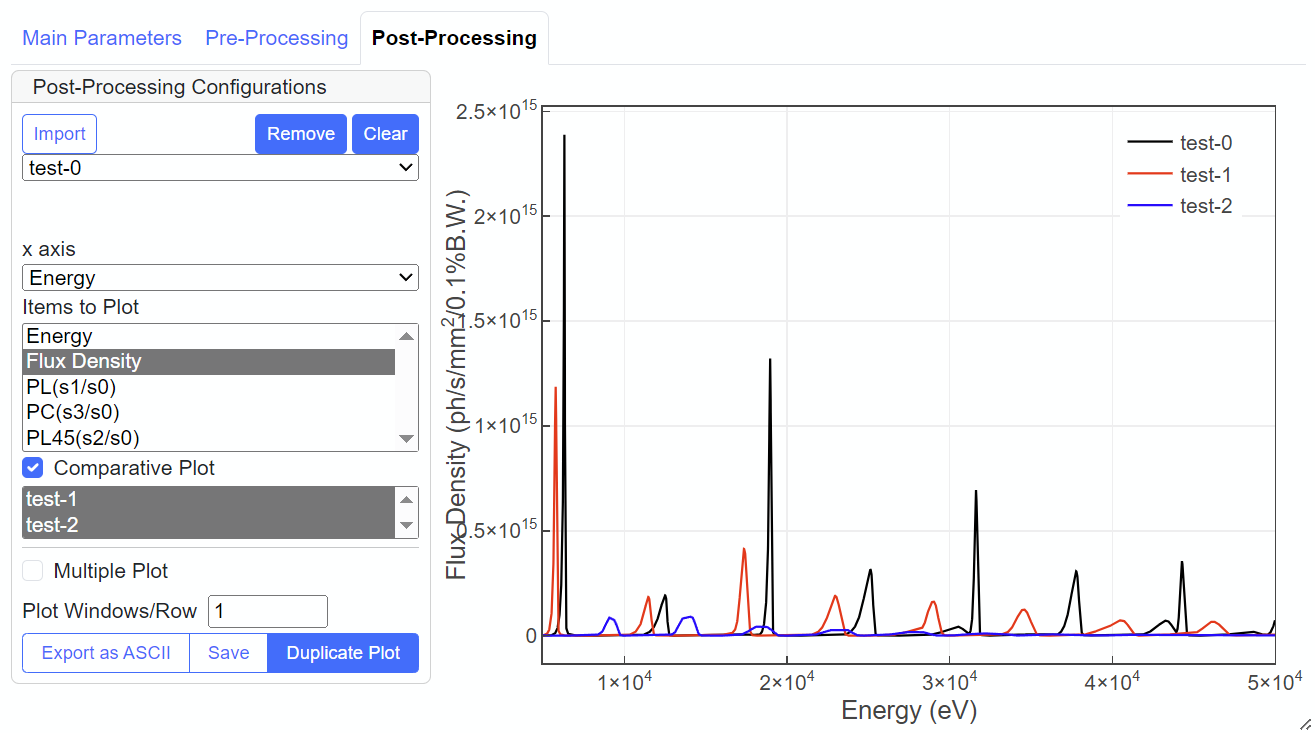
For visualization, select more than one item from "Items to Plot". The dimension of the plot depends on the calculation type of the loaded file. In a 1D plot, a desired area can be zoomed in by dragging. Other options are available to operate the plot, by clicking one of the small icons located in the right top of the plot. For details, refer to the documents about "Plotly" library to be found online.
Besides the above options, the plot can be configured in a dialog panel that appears by clicking a small icon (pencil) located in the top right of the plot. Options available are as follows; switch the scale (linear or log), change the 2D plot type (contour, color-scale surface or shaded surface), or change the method of scaling in each frame for multidimensional plot (see below).
Comparative Plot
If more than one output file with the same calculation type is loaded, "Comparative Plot" is available, and possible data names are shown. Click the desired ones to compare the results. Note that 1D data sets are shown in the same plot, however, 2D data sets are plotted separatory and thus more than one plots are shown. How to arrange the plots can be specified by "Plot Windows/Row" parameter. If there are 6 plots in total and this parameter is set to 3, they are arranged in 3 columns times 2 rows.
Multiple Plot
This option is available for more than two data sets having different calculation types and thus "Comparative Plot" is not available. It tries to create a number of plots and display in the plot area. How to arrange the plots can be specified by "Subplots/Row" parameter. If there are 6 plots in total and this parameter is set to 3, they are arranged in 3 columns times 2 rows.
Plotting 3/4-Dimensional Data
There exist a number of calculation types to generate 3D or 4D output data in SPECTRA (including the Scanning a Parameter option), which cannot be plotted in a straightforward manner. In SPECTRA, the 3D/4D data are "sliced" into a number of data sets and plotted as a 1D or 2D graph. As an example, let us consider the visualization of a Wigner function calculated in the 4D phase space (X,X',Y,Y'). SPECTRA offers several combinations for plotting and slicing variables. If a pair (X,X') is chosen as the plotting variable, then the data is sliced at each (Y,Y') position, and 2D plot (Brilliance vs X,X') is created. Note that the coordinates of the slicing variables can be arbitrary chosen within the possible range, by dragging the sliders indicating their positions.
The post-processed output data can be saved as another JSON file in two methods explained below.
Export as ASCII
The visualization result, or the data set(s) currently plotted, are exported as an ASCII file.
Save
The plot configurations together with the output data are saved in a JSON file. The file can be later imported by the post-processor to reproduce the plot.
Parameter Set
In SPECTRA, parameters and numerical conditions displayed in the "Accelerator", "Light Source" and "Configurations" subpanels are separately saved in JSON objects, each of which is referred to as a Parameter Set. For example, "Accelerator Parameter Set" means a JSON object that stores the parameters displayed in the "Accelerator" subpanel. In addition, "Beamline Parameter Set" is available to bundle the three Parameter Sets, which represent a "beamline" in a specific SR facility. Each Parameter Set can be switched from one to another by selecting from the submenus in "Parameter Set" main menu. To configure (rename, duplicate, or delete) the parameter sets, run Edit menu command. Then a modal dialog box pops up to show the current contents of all the parameter set as shown below.
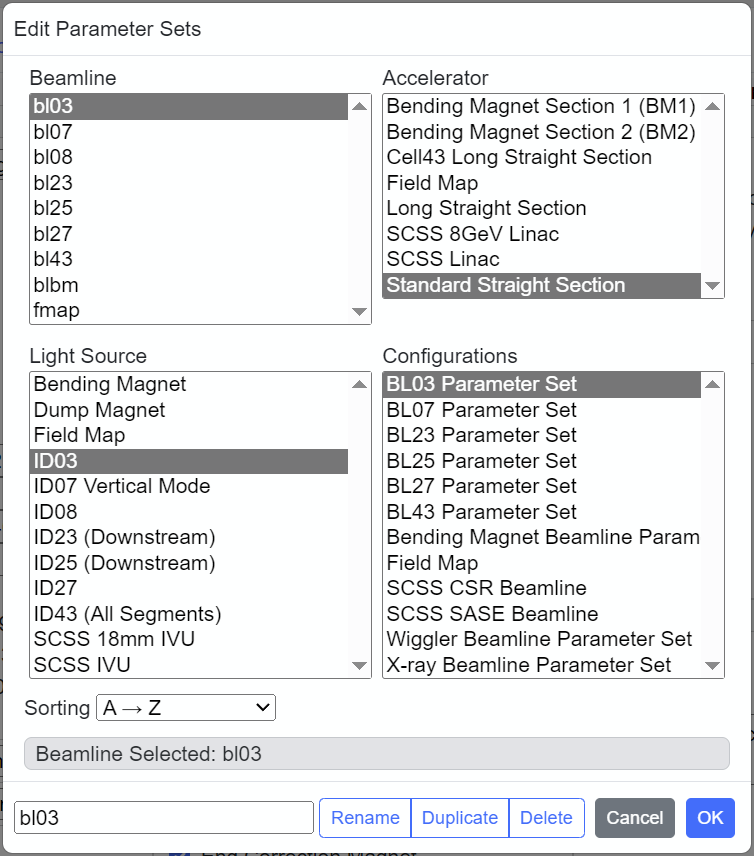
Select the target item for configuration; in the above example, "Beamline bl03" is the target parameter set. Click one of the buttons for operation; for example, to rename or duplicate the parameter set currently in selection, enter a new name in the text entry box in the left bottom and click [Rename] or [Duplicate] button. To delete the parameter set, click [Delete] button; note that at least one parameter set should be left.
Menu Commands
File
| Menu | Details | |
| Create a New Parameter File | Start SPECTRA with a default parameter set. | |
| Open a Parameter File | Open a SPECTRA parameter file. Even though a parameter file for older (≦ 10.2) versions is accepted as well, it cannot be saved in the older format. | |
| Append Parameter Sets | Append the parameter sets in another parameter file to the current ones. | |
| Load Output File | Load the output file of a former calculation. | |
| Open Post-Processed Result | For post-processing (visualization) | |
| Wigner Function for CMD | To perform CMD with the Wigner function | |
| Wigner Function for Wavefront Propagation | To perform Wavefront Propagation with the Wigner function | |
| CMD Result for Modal Profile | For modal analysis with the CMD result | |
| Bunch Factor for Coherent Radiation | Reuse the bunch factors for other coherent radiation calculations | |
| Save | Save all the parameters and options in the current file. | |
| Save As | Save all the parameters and options in a new file. | |
| Exit | Quit SPECTRA and Exit | |
Select Calculation
Select the type of calculation. Refer to Calculation Type for details.
Run
| Menu | Details |
| Create a New Process | Create Calculation Status/Processes with the current parameters and options. |
| Export Calculation Settings | Export the current parameters and options to a file, which can be used as an input file to directly call the solver. |
| Start Calculation | Start a new calculation, or launch the Calculation Status/Processes. |
Parameter Set
Select and edit the "Parameter Set", Refer to Parameter Set for details.
Edit
Open one of the Setup Dialogs to set up various configurations, not included in the Parameter Sets.
Help
Open the reference manual or show the information about SPECTRA.
Setup Dialogs
Open a dialog to edit miscellaneous parameters besides those displayed in the main panel. Details of each dialog are explained below.
| Submenu | Details | ||||||||||||||||||||||||||||||||||||||||
| Filter/Absorber Material |
Open a dialog to edit the material available for the filters and absorbers. 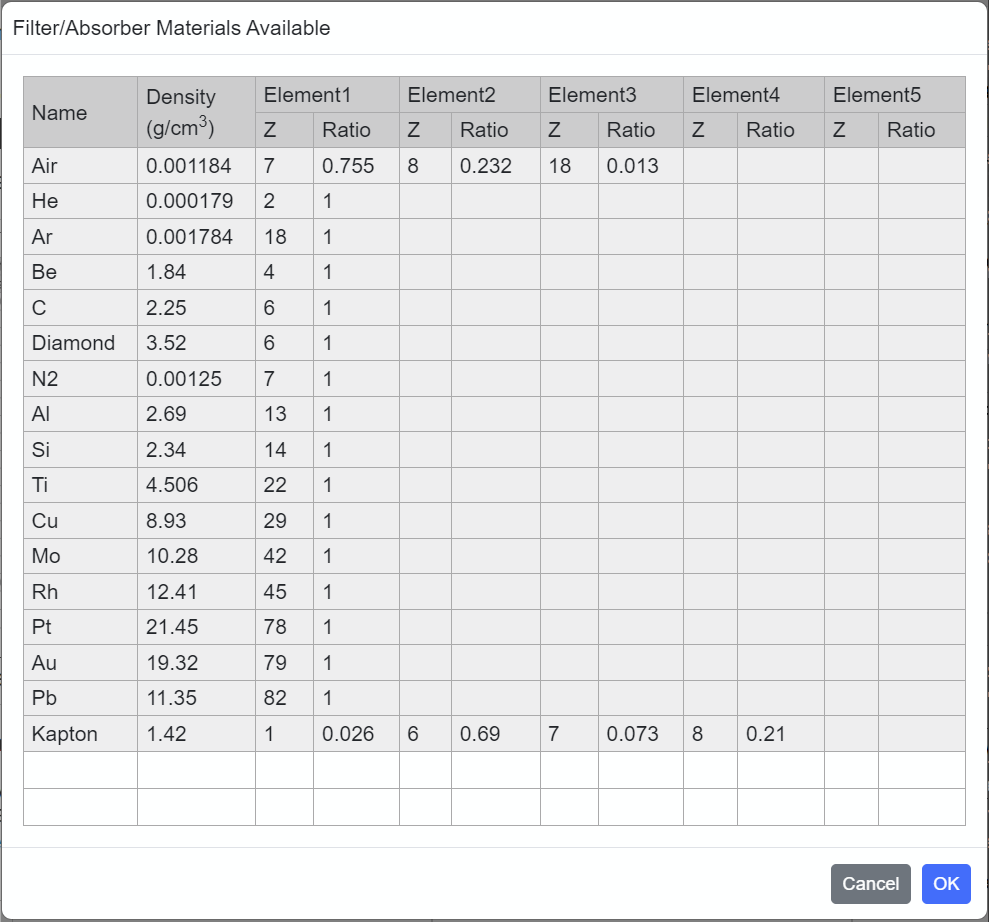 In SPECTRA, a number of built-in materials are available (gray-painted ones), which cannot be edited. To add a new material, input its name and density in an empty column, together with the atomic number (Z) and mass ratio (Ratio) of each element constituting the material. The total amount of the mass ratio should be 1. The numbers of columns (materials) and rows (elements) are automatically increased when necessary. |
||||||||||||||||||||||||||||||||||||||||
| Units for Data Import |
Open a dialog to select the unit of items in the Data Import. 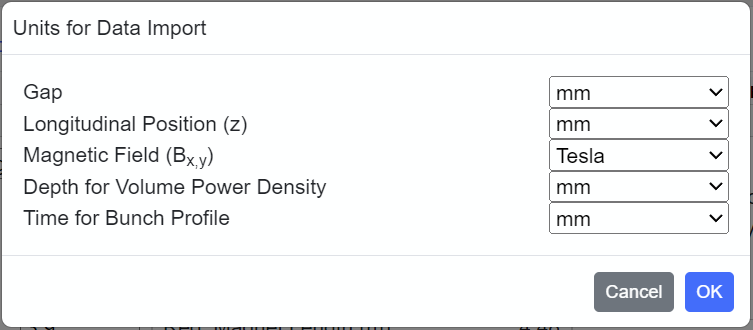 Note that the selection should be made before importing the data. After importing, change of the unit in this dialog has no effect. |
||||||||||||||||||||||||||||||||||||||||
| Numerical Accuracy |
Open a dialog to customize the target numerical accuracy. Note that this menu is not available if "Default" is selected for Accuracy option. There are a number of parameters to specify the numerical accuracy, according to the numerical method and target item. Refer to the table below.
|
||||||||||||||||||||||||||||||||||||||||
| MPI Settings |
Open a dialog to configure the parallel computing. Tick "Enable Parallel Computing" to enable the parallel computing and input a number of processes to launch in "Number of MPI Processes". Note that MPI (message passing interface) environment should be installed for parallel computing, and the path to "mpiexec" should be set. |
||||||||||||||||||||||||||||||||||||||||
Edit the Plot
Besides standard Plotly.js configurations, a number of options to edit the graphical plot in the post- and pre-processors are available. To do so, click the small icon located in the top-right side of the plot. Then a dialog box pops up to let the user edit the plot in the following configurations.
| Item | Details | Available Options |
| Normalize | Select how to normalize the animation plot | For Each: y-/z-axis scale is normalized by the maximum value for each slide |
| By Maximum: y-/z-axis scale is normalized by the maximum value over the whole slides | ||
| X-axis Scale | Select the scale for x axis | Linear, Logarithmic |
| Y-axis Scale | Select the scale for y axis | Linear, Logarithmic |
| Plot Type | Select the type of the 1D plot | Line, Line & Symbol, Symbol |
| Symbol Size | Size of the symbol | Input a number |
| Line Width | Width of the line | Input a number |
| 2D Plot Type | Select the type of the 2D plot | Contour: contour plot with a specific color map |
| Surface (Color Map): surface plot painted with a specific color map | ||
| Surface (Shaded): shaded surface plot illuminated by a specific light source | ||
| Color | Select the color of the light source to create a shaded surface plot | Select from the color picker dialog. |
| Color Map | Select the color map. Several built-in options are available but cannot be customized | Default, Rainbow, Blackbody, Earth, Greys |
| Wireframe | If checked, grid lines are shown on the surface plot |
Parameter List
All the parameters available in the subpanels of the "Main Parameters" panel are summarized below, for each subpanel.
Accelerator
| Parameter/Option | Detail |
| Main Parameters and Conditions | |
| Type | Type of the accelerator. In SPECTRA, the accelerators are categorized into two types: "Storage Ring" and "Linear Accelerator". The difference between them is how to specify the average beam current. In the former, it is directly specified by the user. In the latter, the pulse repetition rate and bunch charge should be given to evaluate the average current. |
| Energy (GeV) | Total energy of the electron beam. |
| Current (mA) | Average beam current of the accelerator. The former is determined by the user, while the latter is evaluated from "Pulses/sec" and "Bunch Charge". |
| Avg. Current (mA) | |
| Circumference (m) | Circumference of the storage ring. |
| Bunches | Number of electron bunches stored in the storage ring. |
| Pulses/sec | Number of electron bunches/second in the linear accelerator. |
| σz (mm) | Bunch length and charge of the electron beam. |
| Bunch Charge (nC) | |
| Nat. Emittance (m.rad) | Natural emittance of the electron beam. |
| Coupling Constant | Coupling constant and energy spread of the electron beam. |
| Energy Spread | |
| βx,y (m) | Twiss parameters at the center of the light source |
| αx,y | |
| ηx,y (m) | Dispersion functions and their derivatives. |
| η'x,y | |
| Peak Current (A) | Peak current of the electron beam evaluated from relevant parameters. |
| εx,y (m.rad) | Horizontal and vertical emittances evaluated from ε and Coupling Constant. |
| σx,y (mm) | Beam size and angular divergence at at the center of the light source. |
| σ'x,y (mrad) | |
| γ-1 (mrad) | Inverse of the Lorentz factor. |
| Injection Condition | |
| Injection Condition |
Specify the injection condition, or the position and angle of the electron beam at the entrance of the light source.
|
| x,y (mm) | Horizontal/vertical positions/angles at the entrance. Available when "Injection Condition" is Custom |
| x',y' (mrad) | |
| Others | |
| Bunch Profile |
Specify the distribution functions of the electron beam in the spatial and temporal domains.
|
| Current Profile | Dictionary data to represent the current profile of the electron bunch. |
| E-t Profile | Dictionary data to represent the electron distribution in the E-t phase space. |
| Particle Distribution | File name to specify the particle coordinates in the 6D phase space (x,x',y,y',t,DE/E) used for "Particle Distribution" option. An example of the data format is shown below. |
| Zero Emittance | Calculation is done without the effects due to the finite emittance and/or energy spread of the electron beam. |
| Zero Energy Spread | |
| Single Electron | SR emitted by a single electron is supposed. |
| Additional R56 (m) | Strength of the virtual dispersive section located in front of the light source. Effective for computation of coherent radiation, if "E-t Profile" is chosen for the electron bunch profile. |
Light Source
| Parameter/Option | Detail |
| Main Parameters | |
| Gap (mm) | Gap of the ID. |
| Bx,y (T) | Field amplitude (IDs) or uniform field (BMs). |
| B (T) | |
| Main Field (T) | Peak fields of the main and sub poles of Wavelength Shifters. |
| Sub Field (T) | |
| λu (mm) | Magnetic Period Length of the ID |
| Device Length (m) | Total length of the ID |
| Reg. Magnet Length (m) | Length of the ID for the regular period. |
| # of Reg. Periods | Number of regular periods. |
| K0x,0y | Available for APPLE undulators. Maximum K values (deflection parameters) when the phase is adjusted to generate horizontal and vertical polarizations. |
| Phase Shift (mm) | Longitudinal shift of each magnetic array for the APPLE undulators, defined as the displacement from the position for the horizontally-polarized mode. To be specific, K values are given as $K_x=K_{x0}\sin(2\pi\Delta z/\lambda_u)$ and $K_y=K_{y0}\cos(2\pi\Delta z/\lambda_u)$, where $\Delta z$ is the phase shift. |
| Kx,y | K values of the ID. |
| K value | |
| K⊥ | Composite K value defined as $\sqrt{K_x^2+K_y^2}$. |
| ε1st (eV) | Fundamental photon energy and wavelength of undulator radiation. |
| λ1st (nm) | |
| Harmonic Component |
Arrange the harmonic components for Multi-Harmonic Undulators.
|
| ρ (m) | Radius of the BM. |
| BM Length (m) | Specify the geometric configuration of BMs. "Origin for CSR" defines the longitudinal coordinate where the electron bunch length or the temporal profile is defined to calculate coherent radiation.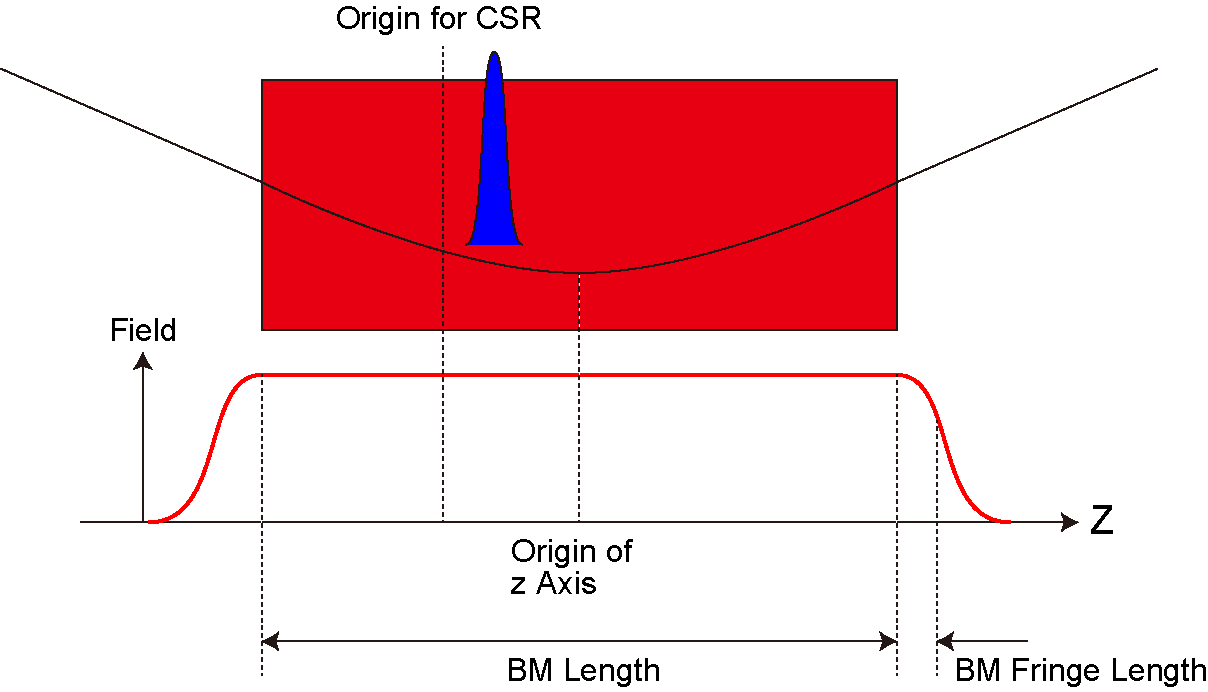 |
| BM Fringe Length (m) | |
| Origin for CSR (m) | |
| Main Length (m) | Lengths of the main and sub poles of the Wavelength Shifter. |
| Sub Length (m) | |
| BM Interval (m) | Distance between two BMs. |
| Field Mapping Data | File name containing the 3D magnetic field data. Refer to Magnetic data format for custom sources for details. |
| σr,r' (mm,mrad) | Natural source size and angular divergence of radiation. |
| σrx,rx' (mm,mrad) | |
| σry,ry' (mm,mrad) | |
| Σx,x' (mm,mrad) | Effective source size and angular divergence of the photon beam, convoluted with those of the electron beam. |
| Σy,y' (mm,mrad) | |
| Flux Density | Approximate values of the on-axis flux density, available flux, and brilliance at ε1st. |
| Flux1st | |
| Brilliance1st | |
| Peak Brilliance | Peak brilliance at ε1st evaluated with the peak current of the electron beam. |
| Bose Degeneracy | Bose degeneracy evaluated for the Peak Brilliance. |
| εc (eV) | Critical photon energy and wavelength. |
| λc (nm) | |
| Total Power (kW) | Total radiation power. |
| Total Power/Rev. (kW) | Total power/revolution and linear power density of the BM. |
| Lin. Pow. Density (kW/mrad) | |
| Options | |
| Gap-Field Relation |
Specify the relation between the gap and peak field of the ID.
|
| APPLE Configuration | Enable/disable the APPLE configuration for Elliptic Undulators. |
| Field Structure |
Specify the field-distribution symmetry of the ID.
|
| Br (T) | Remanent field of the permanent magnet. |
| Geometrical Factor (x,y) | Geometrical factor to reduce the peak magnetic field (x,y). |
| End Correction Magnet | Put additional magnets at the both ends, for orbit compensation. |
| Natural Focusing |
Apply the natural focusing of IDs.
|
| Tandem Arrangement | Calculate radiation from two BMs located at the both ends of the straight section. |
| Parameters for the Field-Error Condition | |
| Field Offset & Taper | Specify if the magnetic field contains an error component. |
| Offset x,y (T) | Magnetic field offset, such as that coming from the ambient field. |
| Lin. Taper x,y (/m) | Linear (a1) and quadratic (a2) taper coefficients. The magnetic field amplitude is given as \[B(z)=B_0(1+a_1z+a_2z^2),\] where $B_0$ is the field amplitude corresponding to the K value. |
| Quad. Taper x,y (/m2) | |
| Parameters to Specify the Phase Error | |
| Add Phase Error | If ticked, the RMS phase error and relevant parameters can be specified. |
| Random Number Seed | Seed for the random number generator to model the field error. |
| σB (%) | RMS of the peak field variation. |
| σφ (deg.) | RMS of the phase error [6]. |
| σx,y (mm); | RMS of the trajectory error. |
| Parameters for the Segmented Undulator Option | |
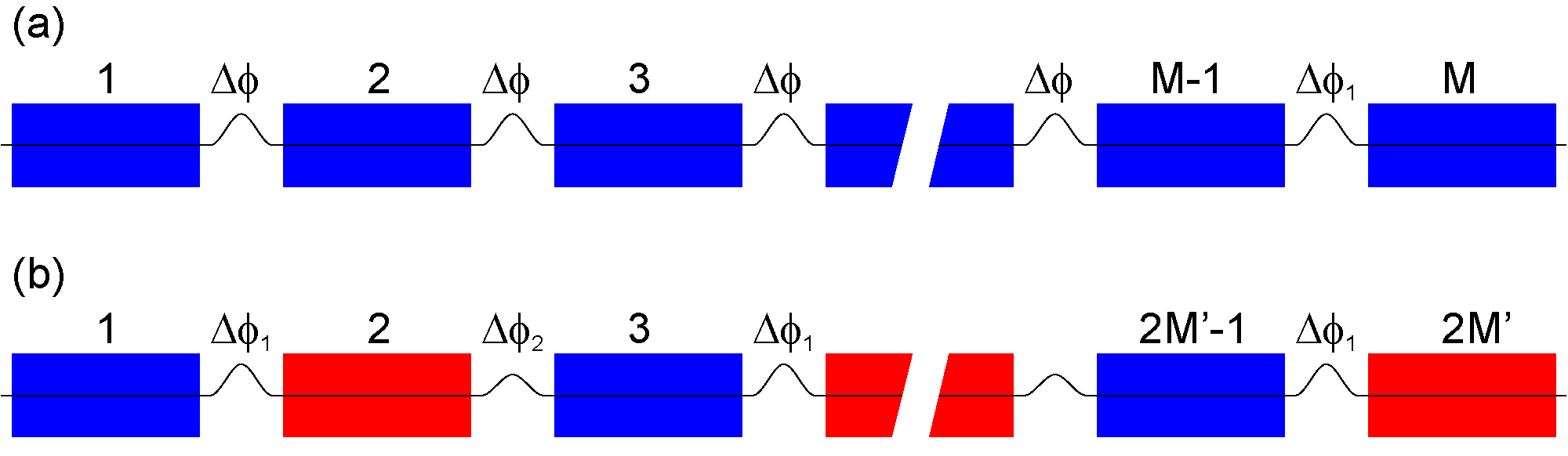
| Segmentation |
Arrange the segmented undulator configuration. For details of how these segmentation schemes work to improve the characteristics of radiation, refer to [7] and [8].
|
| Number of Segments | Number of undulator segments (M) if "Identical" is selected for "Segmentation", or number of segment pair (M') for other options. |
| Half Number of Segments | |
| Segment Interval (m) | Distance between the center positions of adjacent undulator segments. |
| Number of Phase Slip@λ1 | Slippage in the drift section given in the unit of λ1st. |
| Δφ (π) | Additional phase in the unit of π. |
| Δφ1,2 (π) | Additional phase in the unit of π: subscripts 1 and 2 refer to the odd and even drift sections |
| Matching Distance (m) | Distance between virtual focusing magnets in the matching section to arrange the periodic lattice function. |
| Periodic β Function | The betatron function is periodic with the period of segment interval. |
Light Source Type
Details of the type of the light sources available in SPECTRA are summarized below.
| Name | Details | Field Profile |
| Linear Undulator | Conventional linear undulator for horizontal polarization | Sinusoidal |
| Vertical Undulator | Undulator for vertical polarization to generate a horizontal field | |
| Helical Undulator | Undulator for circular polarization to generate a (completely) helical field | |
| Elliptic Undulator | General form of an undulator to generate a helical-like field (horizontal and vertical field amplitudes may be different) | |
| Figure-8 Undulator | Undulator having figure-8 shaped electron orbit, for horizontal polarization and low on-axis heat load | |
| Vertical Figure-8 Undulator | Same as the figure-8 undulator, but for vertical polarization | |
| Multi-Harmonic Undulator | "Semi-Customized" undulator, in which the magnetic field distribution is composed of a number of harmonic components. The strength and phase of each harmonic should be defined by the user. | Custom |
| Bending Magnet | Conventional bending magnet | Uniform |
| Wiggler | Conventional multi-pole wiggler | Sinusoidal |
| EMPW | Elliptic multi-pole wiggler for elliptic polarization in the high energy region | |
| Wavelength Shifter | Wavelength shifter composed of 3 magnet poles; the main (central) pole has the strongest field, while the other two have lower fields so that the field integrals are zero. Note that the magnetic field is not uniform along the longitudinal (z) axis but changes in a sinusoidal manner | Semi Sinusoidal |
| Field Mapping | Specify the 3-D magnetic vector in the (x,y,z) space to calculate the electron orbit. Refer to Magnetic data format for custom sources for details. | Custom |
| Periodic: User Defined | Similar to "Field Mapping", but specify the 2D magnetic vector along z. Refer to Magnetic data format for custom sources for details. | |
| User Defined |
Magnetic data format for custom sources
When one of the custom light sources ("User Defined", "Periodic: User Defined", and "Field Mapping") is chosen, the user should prepare a data file to import the magnetic data. The format of the data file depends on the ligt source and is summarized below.
| Source Type | Format |
| User Defined | |
| Periodic: User Defined | |
| Field Mapping | |
Configurations
| Parameter/Option | Detail |
| Main Parameters | |
| Position x,y (mm) | Transverse position/angle at the observation point. |
| Angle θx,y (mrad) | |
| Energy Range (eV) | Energy range and pitch for Energy Dependence calculations. |
| Energy Pitch (eV) | |
| Energy Pitch for Integration (eV) | Energy pitch for integration in Volume Power Density calculations. Needs to be defined by the user for User Defined light sources. |
| Points (Energy) | Number of energy points for Energy Dependence calculations. |
| Detuning | Photon energy defined as a detuned value, i.e., $\varepsilon/(n\varepsilon_1)-1$, where $n$ is the target harmonic number. |
| Target Energy (eV) | Photon energy to be fixed. |
| Normalized Energy | Same as the above, but normalized by ε1st. |
| Auto Config. for Energy Range | Enable automatic configuration to define the energy range and pitch. |
| Auto Config. for Transverse Range | Enable automatic configuration to define the spatial/angular range and grid intervals. |
| x Range (mm) | Range of the Observation positions/angles for "Spatial Dependence" calculations: (a) [Along Axis] and [Mesh: x-y] and (b) [Mesh: r-φ].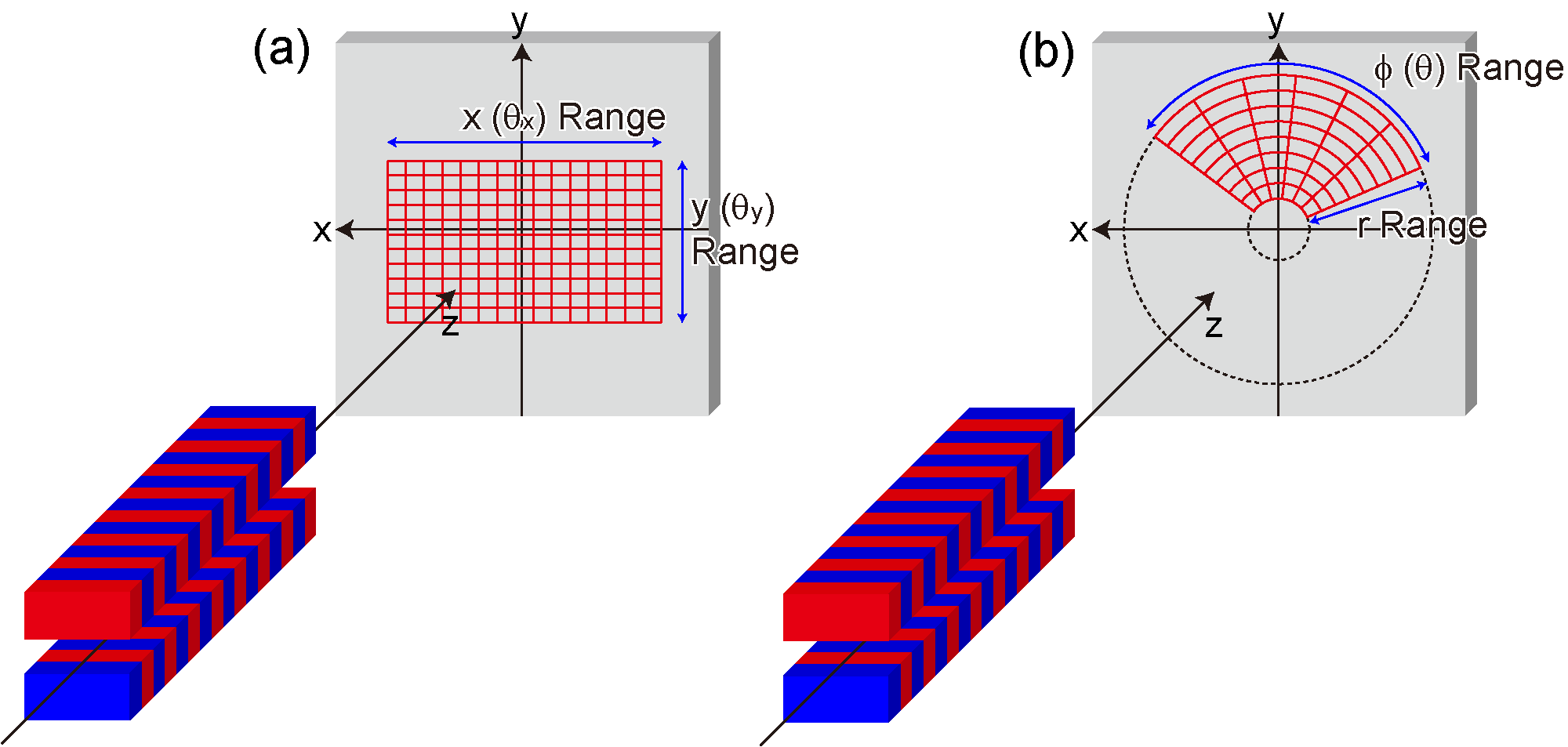 |
| θx Range (mrad) | |
| y Range (mm) | |
| θy Range (mrad) | |
| r Range (mm) | |
| θ Range (mrad) | |
| φ Range (deg.) | |
| Points (x) | Number of observation point in the relevant range. |
| Points (y) | |
| Points (r) | |
| Points (θ) | |
| Points (φ) | |
| Distance from the Source (m) | Distance from the center of the light source to the observation point. |
| Slit Pos.: x,y (mm) | Specify the configuration of the slit positions and aperture.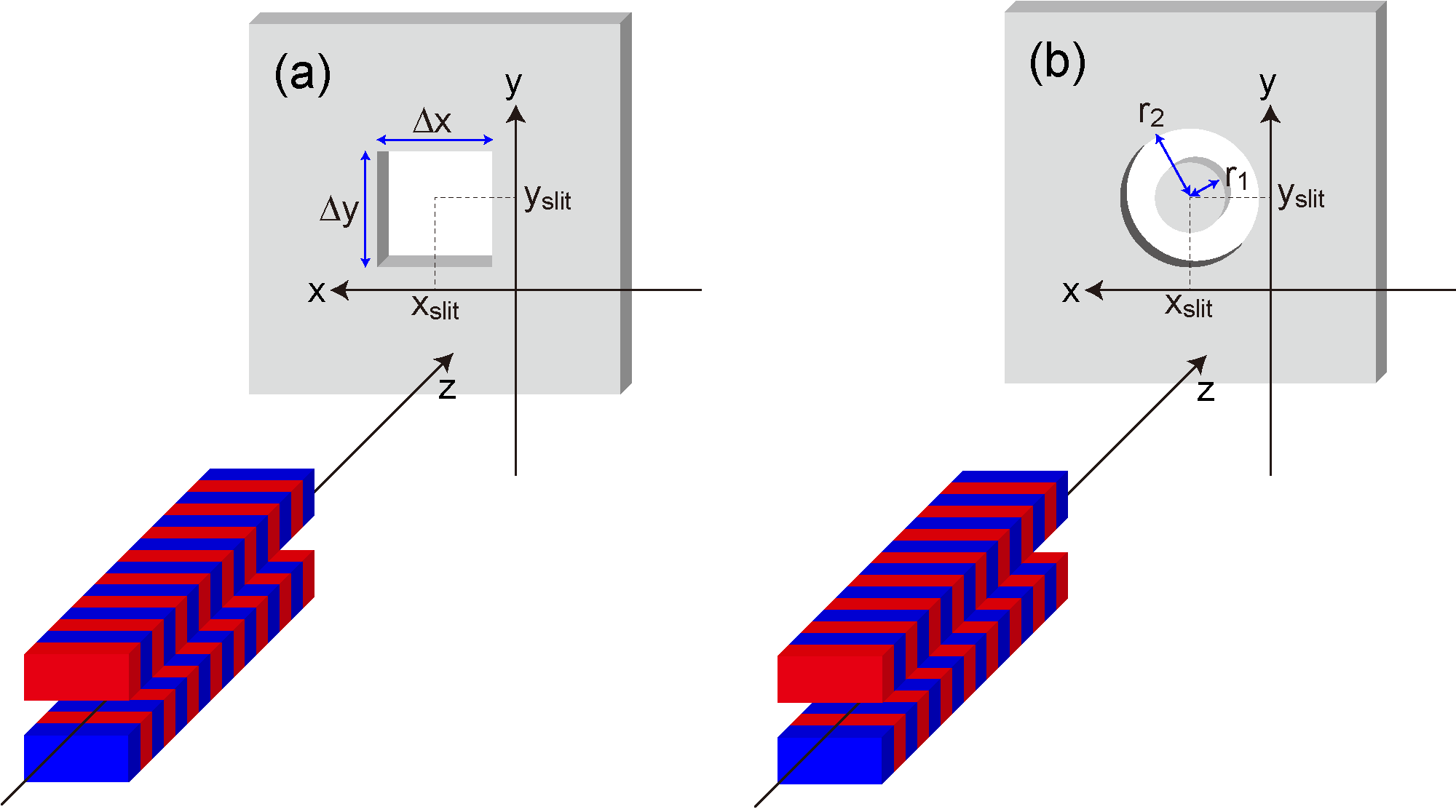 |
| Slit Pos.: θx,y (mrad) | |
| Δ/Σs: x,y | |
| Δx,Δy (mm) | |
| Slit r1,2 (mm) | |
| Slit θ1,2 (mrad) | |
| Depth Range (mm) | Depth range and number of points for Volume Power Density calculations. |
| Points (Depth) | |
| Δθx,y (mrad) | Angular acceptance to confine the photon beam and resultant illuminated area of the object, and angles to define the condition of glancing incidence for Volume Power Density calculations. |
| Illuminated x,y (mm) | |
| Glancing Angle (deg.) | |
| Azimuth of Incidence (deg.) | |
| x Range (mm) | Position of the object and range of observation for Spatial Power Density calculations. Note that SPECTRA distinguishes the inner and outer sides of the surface. To be specific, the above figure shows the case when the inner size indicated by a red line is facing the beam axis, and thus receives the radiation power. If, in contrast, the object with the same normal vector is located at a negative position of x, the inner surface is facing outsize and it does not receive any radiation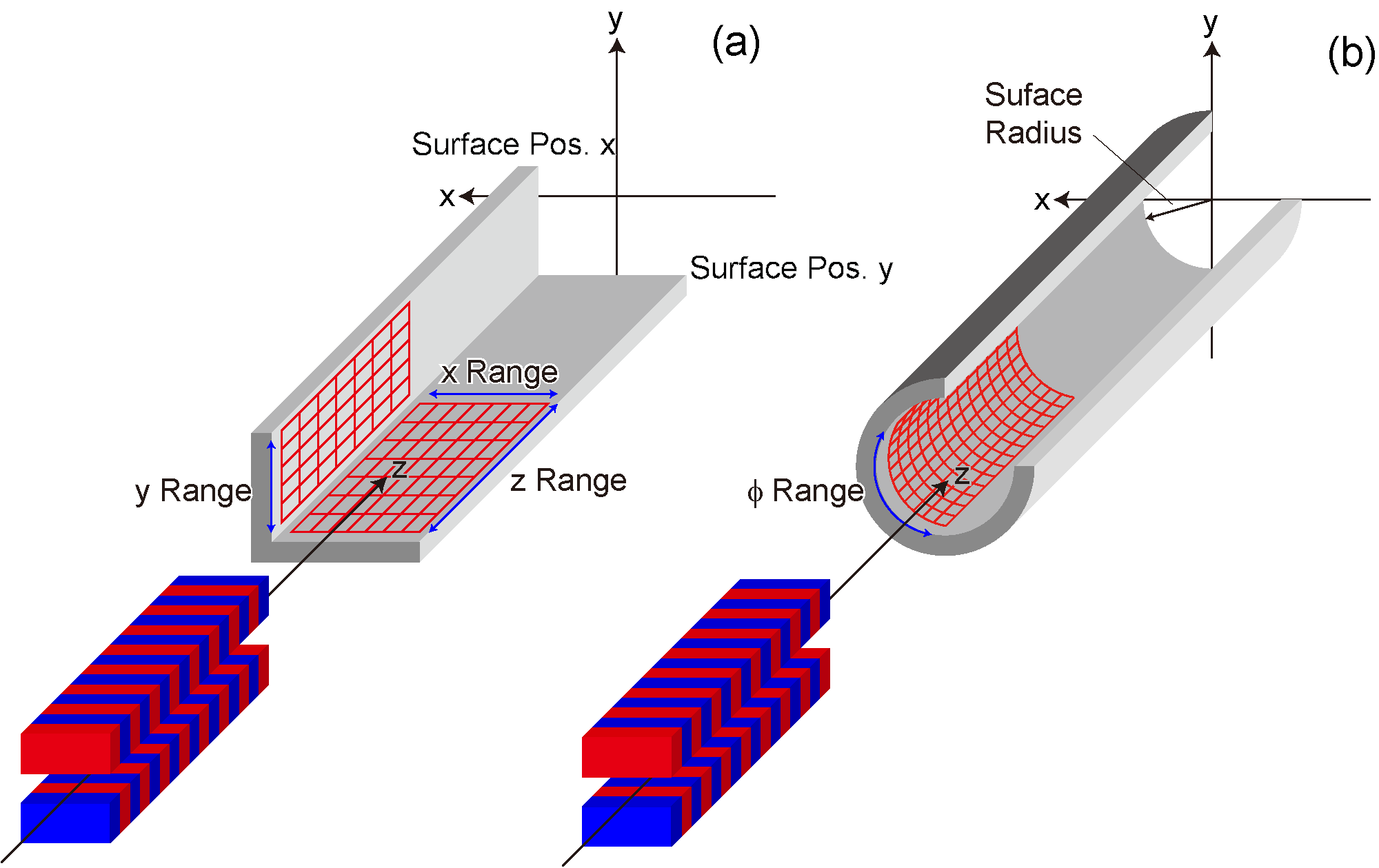 |
| y Range (mm) | |
| z range (m) | |
| Surface Pos. x (mm) | |
| Surface Pos. y (mm) | |
| Surface Radius (mm) | |
| Points (x) | Number of observation points in the relevant range |
| Points (y) | |
| Points (z) | |
| Θ (deg.) | Normal vectors to specify the inner surface of the object irradiated by SR. In "Fixed Point Calculation" calculations, the normal vector to the object surface is specified more flexibly by two angles as schematically illustrated below. For example, Θ = Φ = 0 means that the surface of the object is parallel to the y-z plane, with its inner side facing the beam axis. Angles of the normal vector to define the inner surface illuminated by radiation for Spatial Power Density calculations.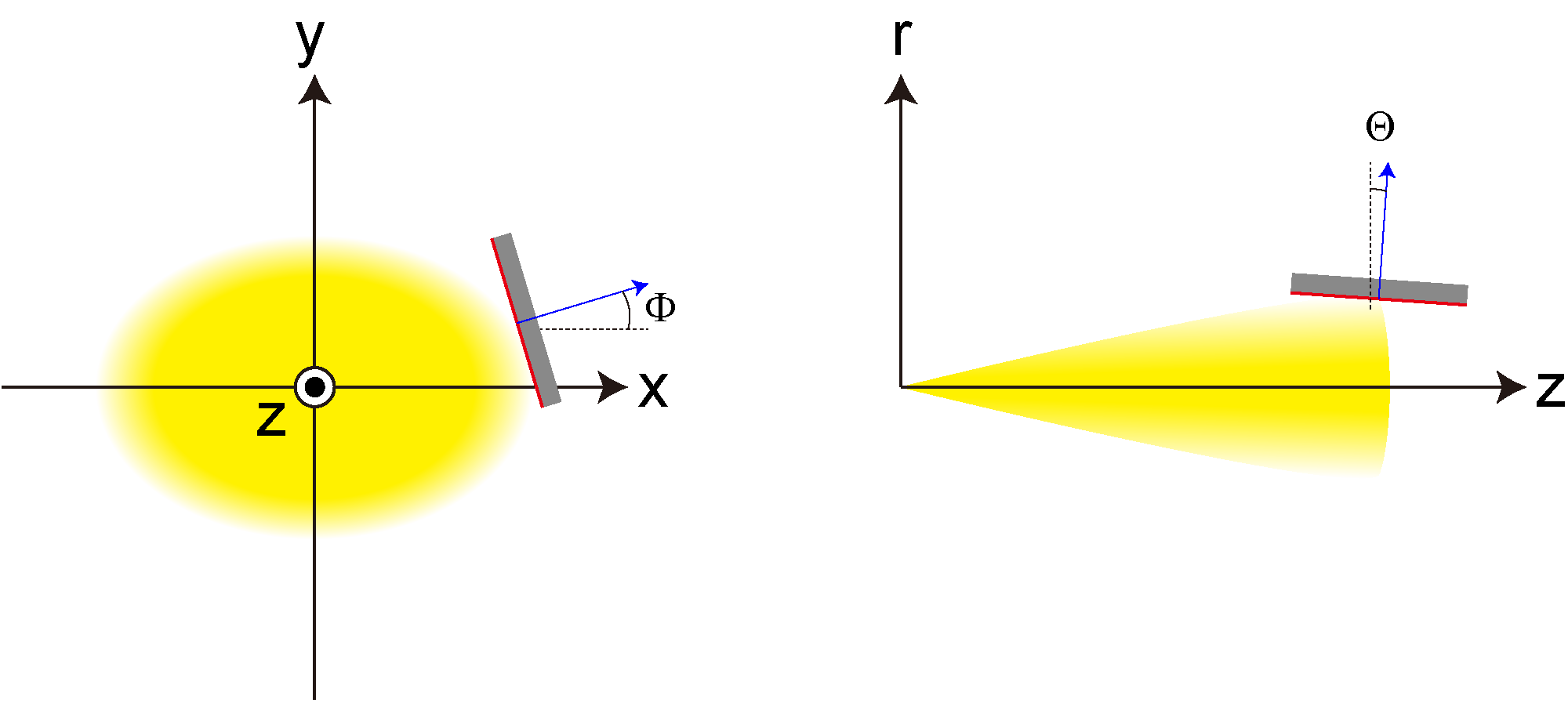 |
| Φ (deg.) | |
| Σx,y@ε1st (mm) | Photon beam size and divergence at the observation position, defined at ε1st. Note this is a rough estimation and does not take into account the energy spread of the electron beam. |
| Σx',y'@ε1st (mrad) | |
| Σpx,py (mm) | Spatial spread and divergence of the radiation power at the observation position |
| Σpx',py' (mrad) | |
| K Range | Range of the K values and number of points. |
| K⊥ Range | |
| Points (K) | |
| ε1st Range (eV) | Range of the fundamental energy determined by the above K-value range. |
| Power Upper Limit (kW) | Upper limit of the partial power to define the width and height of the rectangular slit for K Dependence calculations. |
| Harmonic Range | Harmonic range or target harmonic number for K-value dependence calculations. |
| Target Harmonic | |
| Temporal Range (fs) | Temporal range and number of points for Time Dependence calculations. |
| Points (Temporal) | |
| Maximum Harmonic | Maximum harmonic number to be considered. |
| Slice X (mm) | Transverse positions and angles at the source point where the Wigner function is calculated. These parameters should be distinguished from those indicated by lower letters, which mean the transverse positions at a certain longitudinal position downstream of the light source. |
| Slice Y (mm) | |
| Slice X' (mrad) | |
| Slice Y' (mrad) | |
| X Range (mm) | Calculation range/number of points of the transverse positions/angles at the source point. Should be distinguished from those indicated by lower letters (see above). |
| Points (X) | |
| X' Range (mrad) | |
| Points (X') | |
| Y Range (mm) | |
| Points (Y) | |
| Y' Range (mrad) | |
| Points (Y') | |
| γΔθx,y | Angular acceptance normalized by γ-1 to calculate the Wigner function. |
| X' Acceptance (mrad) | |
| Optical Element | Optical element to be inserted. |
| Position (m) | Position of the optical element. |
| Aperture x (mm) | Aperture size of the slit. |
| Aperture y (mm) | |
| Slit Distance x (mm) | Distance of the double slit. |
| Slit Distance y (mm) | |
| Soft Edge Fringe Size (mm) | Length of the soft-edge region. |
| Limit of Diffraction Effect | Target tolerance to define the threashold of the angular range when a slit is inserted. |
| Larger Angular Range | An integer to define the angular range to evaluate the CSD. |
| Larger Angular Range | An integer to define the angular range to evaluate the CSD. |
| Larger Angular Range | An integer to define the angular range to evaluate the CSD. |
| Focal Length x (m) | Focal length of the thin lens. |
| Focal Length y (m) | |
| Angular Profile | Export the angular profile |
| Wigner Function | Export the Wigner function after the optical element. |
| Cross Spectral Density | Export the CSD. |
| Degree of Coherence | Export the spatial degree of coherence. |
| Options | |
| Filtering |
Specify the type of filtering.
|
| Energy Step |
Specify how to change the energy/depth position in the calculation range.
|
| Depth Step | |
| Slit Aperture Size |
Specify how to represent the width and height of the rectangular slit.
|
| Define Obs. Point in |
Specify how to represent the transverse observation points.
|
| Normalize Photon Energy | Specify the photon energy as a normalized value. |
| Set Upper Limit on Power | Put an upper limit on the allowable partial power. |
| Optimize ΔX' for Computation | Horizontal angular acceptance is virtually closed to reduce the computation time, without changing the calculation results. |
| Level of Smoothing Along X | Apply smoothing for the Wigner function of BMs and wigglers; larger values results in more smooth profiles. |
| Observation in the Fourier Plane | Calculation is done at the "Fourier Plane" as schematically illustrated below, to evaluate the angular profile at the source point (center of the light source)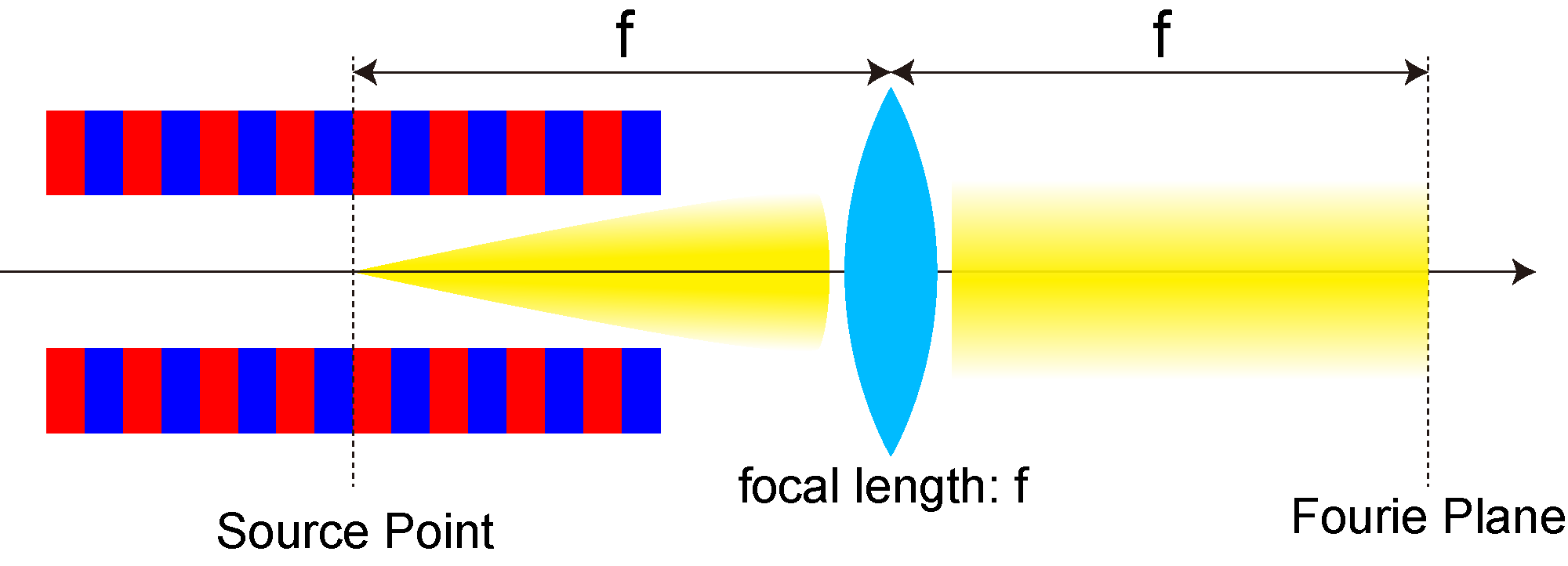 |
| Wiggler Approximation | Apply the wiggler approximation, in which radiation incoherently summed up (as photons). |
| Spectral Smoothing | Apply the spectral smoothing; this is useful to reduce the computation time by smoothing the spectral fine structure potentially found in undulator radiation. |
| Smoothing Window (%) | Smoothing window in %; this means that the photon flux at 1000 eV is given as the average from 995 to 1005 eV. |
| Accuracy | Specify the numerical accuracy. In most cases, "Default" is recommended, in which case SPECTRA automatically arranges all the relevant parameters. If "Custom" is selected, the user should configure each parameter. Refer to Numerical Accuracy for details. |
| Parameters to Specify the BPF | |
| Central Energy (eV) | Central photon energy of the bandpath filter (BPF). |
| Width (eV) | Full width of the boxcar-type BPF. |
| Width (σ, eV) | 1σ of the Gaussian BPF. |
| Max. Trans. Rate | Maximum transmission rate of the BPF. |
| Parameters for the CMD (coherent mode decomposition) | |
| Perform CMD? | Perform "Coherent Mode Decomposition" after calculating the Wigner function. |
| Export Field Profile |
Calculate and export the modal profiles based on the CMD results
|
| Export Intensity Profile | Calculate and export the modal intensity profiles based on the CMD results |
| Compare Wigner Function | Reconstruct the Wigner function using the CMD result to check its validity. |
| Compare Intensity Profile | Reconstruct the flux density profile using the CMD result to check its validity. |
| Apply GS Model | Use Gaussian-Schell (GS) model to simplify the CMD and reduce computation time. |
| GS Model X/Y |
Use Gaussian-Schell (GS) model for CMD. Select the axis to apply.
|
| HG Order Limit (X,Y) | Upper limit of the order of the Hermite-Gaussian functions to be used in the CMD. |
| HG Order Limit (X) | |
| HG Order Limit (Y) | |
| Max. HG Order (X,Y) | Maximum orders of the coherent mode. |
| Max. HG Order (X) | |
| Max. HG Order (Y) | |
| Maximum CMD Order | Maximum number of the coherent modes for post-processing (exporting the modal profile, reconstructing the Wigner functions). |
| Flux Cutoff | Cutoff flux (normalized) to be used to determine the maximum HG order of of each coherent mode. |
| Amplitude Cutoff | Cutoff amplitude (normalized) of individual modes, below which Hermite-Gaussian functions are neglected. |
| Range: X,Y (mm) | Range of the spatial grid to export the modal profile. |
| Range: X (mm) | |
| Range: Y (mm) | |
| Step: X,Y (mm) | Intervals of the spatial grid points to export the modal profile. |
| Step: X (mm) | |
| Step: Y (mm) | |
| Parameters for the FEL mode | |
| FEL Mode |
Coherent radiation in an FEL (free electron laser) mode is calculated. If this option is enabled, interaction (energy exchange) between electrons and radiation is taken into account in solving the equation of electron motion in the 6D phase space."Reuse Bunch Factor": reuse the bunch factor evaluated in the former calculations. This option is available by opening a former calculation result of coherent radiation, with the FEL mode option enabled. |
| Pulse Energy (mJ) | Seed pulse energy. |
| Wavelength (nm) | Seed wavelength. |
| Pulse Length (FWHM, fs) | Seed pulse length. |
| TL. Pulse Length (FWHM, fs) | Transform-limited pulse length of the chirped seed pulse. |
| Source Size (FWHM, mm) | Seed source size. |
| Waist Position (m) | Longitudinal position where the seed pulse forms a beam waist. |
| Timing (fs) | Relative time of the seed pulse with respect to the electron beam. |
| GDD (fs2) | Group delay dispersion and third order dispersion of the chirped seed pulse. |
| TOD (fs3) | |
| Pulse Energy: 1,2 (mJ) | Pulse energies of the 1st and 2nd seed pulses. Available when "Seeded with Double Pulse" is chosen. Note that there are a number of parameters having the same suffix (1,2), which denotes that they are for the 1st and 2nd seed pulses. |
| Step: Initial, Interval (m) | Define the longitudinal step to solve the FEL equation. Refer to the schematic drawing for details.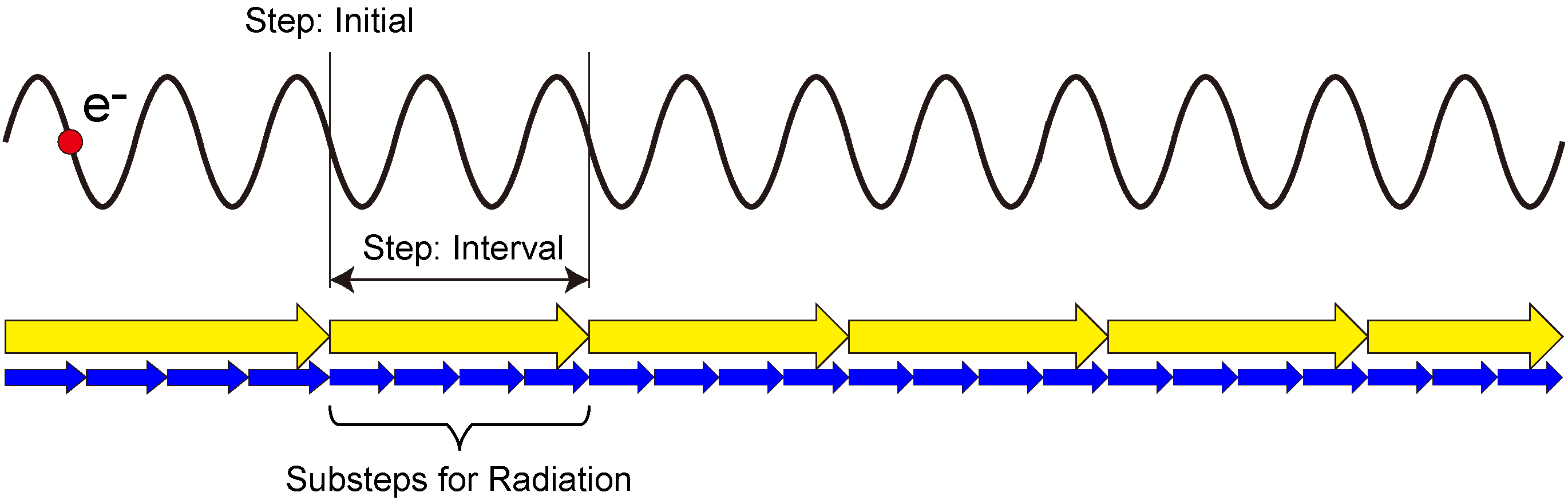 |
| Substeps for Radiation | |
| Photon Energy ROI (eV) | Photon energy range of interest to solve the FEL equation. |
| Number of Particles | Number of macro-particles to represent the electron beam. |
| e- Energy Interval | Interval of the electron energy deviation to export the electron density in the (E-t) phase space. |
| R56 (m) | Strength of the virtual dispersive section. Need to be specified if Bunch with Dispersion option is enabled. |
| Export Intermediate Data | Export the intermediate data evaluated during the process of solving the FEL equation. |
| Bunch with Dispersion | Export the bunch profile after the electron beam passes through a virtual dispersive section located downstream of the source, as in the high-gain harmonic generation (HGHG) FELs. |
| E-t Data | Export the electron density in the (E-t) phase space. |
| Parameters for the wavefront propagation | |
| Transverse Grid |
Specify the transverse grid at each longitudinal step.
|
| Finer Spatial Grid | Specify a finer grid interval if "Automatic"is selected for "Transverse Grid". Default is 0 and a larger number means a finer interval. |
| Optical Element |
Specify an optical element inserted in the beamline.
|
| Position (m) | Longitudinal position to insert an optical element. |
| Aperture x (mm) | Horizontal aperture size. |
| Slit Distance x (mm) | Distance between the double slit in the horizontal direction. |
| Aperture y (mm) | Vertical aperture size. |
| Slit Distance y (mm) | Distance between the double slit in the vertical direction. |
| Soft Edge Fringe Size (mm) | Range of the "Soft Edge"of the slit. At the edge of the slit, the photon intensity is supposed to gradually drop, as opposed to a hard-edged condition. Longer soft-edge ranges reduce the diffraction effects. In addition, the memory requirement is relaxed as well. |
| Limit of Diffraction Effect | Specify the threshold to cut off the diffraction effects and determine the angular range to compute the Wigner function after passing through a slit. |
| Required Memory (MB) ~ | Approximate memory size needed during the computation. The parameters should be arranged so that this value is not too large. |
| Focal Length x (m) | Focal length of an ideal lens in the horizontal direction. |
| Focal Length y (m) | Focal length of an ideal lens in the vertical direction. |
| Larger Angular Range | Specify the angular range to evaluate the Wigner function after an optical element. If set to 0, the angular range is determined to be consistent with the relevant parameters; a larger number means a large angular range. |
| Wigner Function | Export the Wigner function after an optical element. |
| Angular Profile | Export the angular profile after an optical element. |
| Cross Spectral Density | Export the cross spectral density. |
| Degree of Coherence | Export the degree of spatial coherence. |
Binary Format for the Modal Profile
The binary format to export the modal profile is defined below.
- Integer (4 byte) $\times\:3$: $N_m$, $N_X$, $N_Y$
- Double (8 byte) $\times\:2$: $\Delta X$, $\Delta Y$
- Double (8 byte) $\times\:N_XN_Y$: 0-th Mode Profile Real Part
- Double (8 byte) $\times\:N_XN_Y$: 0-th Mode Profile Imaginary Part
- ...
- Double (8 byte)$\times N_XN_Y$: ($N_m$-1)-th Mode Profile Imaginary Part
where $N_m$ is the number of coherent modes, $\Delta X$ and $N_{X}$ are the interval and number of positions along the horizontal (X) axis, and similar expressions for the vertical (Y) axis. The order index j in each array representing the real/imaginary part of the complex amplitude is given as \[j=j_x+j_yN_X\] where $j_x$ and $j_y$ refer to the order indices corresponding to the X and Y positions. To be specific, the X index changes first.
Calculation Setup
Details of how to setup and start the calculations are presented here, together with explanations of the type of calculations and output items available in SPECTRA.
General Method
Open a Parameter File
Upon being started, SPECTRA tries to load parameters from the parameter file that was opened last time. If successful, the parameters are shown in the "Main Parameters" panel. If SPECTRA is run for the first time after installation, default parameters will be shown. To open a new SPECTRA parameter file, run [File]-[Open a Parameter File] command. In the initial setting, the parameter files are found in the directory "[SPECTRA Home]/prm" with a default suffix "json", where "[SPECTRA Home]" is the directory in which SPECTRA has been installed.
Select a Calculation Type
Before starting any calculation, "Calculation Type" should be selected by running one of the submenus in [Select Calculation]. Refer to Calculation Type for details of each calculation type.
Arrange the Output File
Arrange the output file to save the calculation results in the Output File subpanel.
Start Calculation
Run [Run]-[Start Calculation] command to start a single calculation. Then "Calculation Status/Processes" subpanel is displayed in the "Main Parameters" panel to indicate the progress of calculation. To cancel the calculation, click "Cancel" button. Note that the serial number is automatically incremented once the calculation is started, unless it is not negative (-1). This is to avoid the overlap of the output file name in performing successive calculations. When the calculation is completed, the "Calculation Status/Processes" subpanel vanishes and the result is imported in the "Post-Processing" panel for visualization.
Verify the Result
Upon completion of a calculation, the output file is automatically loaded and one of the items is plotted in the "Post-Processing" subpanel to quickly view the results. Refer to Post-Processing for details about how to operate the post-processor.
Calculation Type
To start any calculation in SPECTRA, the "Calculation Type" should be specified first. This is shown as the submenus of [Select Calculation] main menu in the GUI. The meanings and details of the submenus are summarized in the table below. After selection, the calculation type is shown in the top of the "Configurations" subpanel, which is represented by a string given by concatenating a number of submenu items. Note that a "double colon (::)" is inserted between items for clarity.
| Category | GUI Menu Items | Details |
| Numerical Scheme | Far Field & Ideal Condition | Assumes that $|\boldsymbol{R}|$ is much larger than $|\boldsymbol{r}|$, where $\boldsymbol{R}$ and $\boldsymbol{r}$ represent the vectors directing from the origin to the observer and moving electron, respectively. This implies that the observation angle, i.e., an angle formed by $\boldsymbol{R}$ and $\boldsymbol{r}$, is kept constant while the electron passes through the SR source. In addition, the field distribution of the SR source is assumed to be ideal: perfectly periodic in undulators and wigglers, and constant in bending magnets. This significantly simplifies the expressions on SR and thus enables a fast computation. For most applications, such as evaluation of the photon flux passing through a slit and heat load on optical elements, this method is recommended and is in fact reliable enough. |
| Near Field | No approximation is made in this method besides an assumption that the electron is relativistic. In other words, the observation angle is a function of the electron position, i.e., it varies while the electron travels along the SR source axis. If the distance between the SR source and observer is shorter and or comparable to the length of the SR source itself, the near-field effect would not be negligible. Especially, the off-axis spectrum will be considerably different from that observed at the point infinitely far from the SR source. In addition, this method should be chosen if the SR source is not ideal. One important case is to compute the characteristics expected in a real device based on a magnetic field distribution actually measured. | |
| Coherent Radiation | Same as "Near Field", except that the radiation is temporally coherent. In other words, radiation emitted by each electron in the electron beam is summed up coherently. This is in contrast to the two methods described above, where radiation is summed up incoherently. The intensity of coherent radiation is significantly enhanced if the bunch length of the electron beam is shorter than the wavelength of radiation, or it has a local density modulation with the typical length shorter than the wavelength. | |
| Characterization at the Source Point | Evaluates the photon distribution exactly at the source point, or the center of the SR source. This means that the distance from the source to the observer is zero, i.e., $\boldsymbol{R}=\boldsymbol{0}$. Computing the SR properties under such a condition is not possible in a straightforward manner, but requires another numerical operation to propagate the radiation from the observation point back to the source point. SPECTRA is equipped with a number of numerical methods to enable this function. | |
| Fixed Point Calculation | Calculation is performed for a single fixed condition (photon energy, observation point, etc.) and the results are displayed in the GUI. | |
| Coherent Mode Decomposition | Using the photon distribution at the source point (Wigner functions), partially-coherent radiation can be decomposed into a number of coherent modes, which is useful to describe the propagation of SR in the framework of wave optics. | |
| Method | Energy Dependence | Target items are calculated as a function of the photon energy. |
| Spatial Dependence | Target items are calculated as a function of the observation point. | |
| K Dependence | Target items are calculated as a function of the undulator K value (deflection parameter). | |
| Time Dependence | Target items are calculated as a function of time. | |
| Wigner Function | Photon density in the 2D/4D phase space is evaluated by means of the Wigner function method. | |
| Main Target Item | Angular Flux Density | Photon flux per unit solid angle. |
| Spatial Flux Density | Photon flux per unit area. | |
| Partial Flux | Photon flux of radiation passing through a finite aperture. | |
| Total Flux | Photon flux of radiation integrated over the whole solid angle. | |
| Angular Power Density | Radiation power per unit solid angle. | |
| Spatial Power Density | Radiation power per unit area. | |
| Partial Power | Radiation Power passing through a finite aperture | |
| Resolved Power Density | Radiation power decomposed into polarization and harmonic components | |
| Surface Power Density | Radiation power density under a glancing-incidence condition | |
| Volume Power Density | Radiation power per unit volume absorbed by a target object (absorber) | |
| Electric Field | Temporal profile of electric field of radiation. | |
| Complex Amplitude | Spatial profile of complex amplitude of radiation. | |
| Spatial Profile | Transverse profile of the spatial flux density calculated at the source point. | |
| Phase-Space Distribution | Distribution of the photon density in the in the 2D/4D phase space. | |
| CMD with the Wigner Function | Perform CMD using the existing Wigner function data | |
| Modal Profile | Perform post-processing using the CMD results | |
| Condition | Rectangular Slit | Radiation passes through a rectangular aperture. |
| Circular Slit | Radiation passes through a circular aperture. | |
| Along Axis | Moves the observation point along the x- and y-axes. | |
| Mesh: x-y | Moves the observation point over the rectangular grid. | |
| Mesh: r-φ | Moves the observation point over the grid in the 2D polar coordinate. | |
| Simplified Calculation | Assumes that the radiation is a Gaussian beam, and roughly estimates its characteristics, such as the brilliance, on-axis flux density, source size and angular divergence without actually doing the convolution. | |
| Flux at a Fixed Energy | Calculates the characteristics of UR at a fixed photon energy. To be specific, the monochromator is unchanged, while the K value is tuned. | |
| Peak Flux Curve | Calculates the characteristics of UR at peak harmonic energies. To be specific, the monochromator is scanned synchronously with the K value. | |
| Power | Calculate the radiation power as a function of the K value. | |
| Planar Surface: x-z | Calculation is done on the x-z surface located vertically off the beam axis. | |
| Planar Surface: y-z | Calculation is done on the y-z surface located horizontally off the beam axis. | |
| Cylindrical Surface | Calculation is done on the inner surface of a pipe coaxially located with the beam axis. | |
| X-X' (Sliced) | 4D Wigner function calculated on (X,X') phase space at given (Y,Y'). | |
| X-X' (Projected) | 2D (projected) Wigner function calculated on (X,X') phase space. | |
| Y-Y' (Sliced) | 4D Wigner function calculated on (Y,Y') phase space at given (X,X'). | |
| Y-Y' (Projected) | 2D (projected) Wigner function calculated on (Y,Y') phase space. | |
| X-X'-Y-Y' | 4D Wigner function calculated on (X,X',Y,Y'). | |
| Sub-Condition | Target Harmonics | Calculation is performed for individual harmonics. |
| All Harmonics | Optimizes the harmonic number to maximize the target item (brilliance or flux). | |
| Sliced | 4D (X,X',Y,Y') Wigner function at a single point. | |
| Projected on X-X' | 2D Wigner function projected on (X,X'). | |
| Projected on Y-Y' | 2D Wigner function projected on (Y,Y'). | |
| Related Characteristics | Degree of Coherence and X-Y Separability evaluated from Wigner function. |
Output Items
The output items specific to respective calculation types are summarized below.
| Parameter/Option | Detail |
| Flux Density | Spatial (far field conditions) or angular (others) flux density |
| Flux | Partial photon flux passing through a finite angular acceptance, or total flux integrated over the whole solid angle |
| GA. Brilliance | Photon density in the 4D phase space (or its maximum). "GA." stands for "Gaussian Approximation", meaning that it is evaluated by assuming that the photon beam is a Gaussian one. |
| Brilliance | |
| Prj. Brilliance | Brilliance projected on the (X,X') or (Y,Y') phase space. |
| PL(s1/s0) | Stokes parameters: PL, PC, PL45 correspond to the horizontal, left-hand and 45-deg.-inclined linear polarizations. |
| PC(s3/s0) | |
| PL45(s2/s0) | |
| Harmonic Energy | Photon energy of a target harmonic. "Harmonic" is defined as nε1st, where n is the harmonic number, while "Peak" specifies the photon energy at which the photon intensity (flux density of flux) becomes the maximum; in general this is slightly lower than the former one. |
| Peak Energy | |
| Power Density | Spatial (far field conditions) or angular (others) power density |
| Partial Power | Partial power passing through a finite angular acceptance, or total power integrated over the whole solid angle |
| Total Power | |
| Harmonic Power (x) | Angular power density corresponding to a specific harmonic and polarization state |
| Harmonic Power (y) | |
| Volume Power Density | Refer to Volume Power Density |
| Natural Size | Source size and angular divergence of radiation emitted by a single electron |
| Natural Divergence | |
| Horizontal Size | Source size of a photon beam emitted by an electron beam with finite emittance and energy spread |
| Vertical Size | |
| Horizontal Divergence | Angular divergence of a photon beam |
| Vertical Divergence | |
| Coherent Flux | Photon flux contained in a coherent volume of radiation that is fully coherent in space |
| Coherent Power | Power contained in a bandwidth corresponding to 1 μm coherence length |
| Horizontal Coherent Fraction | Quality of a photon beam in terms of coherence, defined as $\Sigma_x\Sigma_{x'}/(\lambda/4\pi)$ for the horizontal direction and a similar expression for the vertical direction, where $\Sigma_{x}$ and $\Sigma_{x'}$ are the source size and angular divergence of the photon beam. |
| Vertical Coherent Fraction | |
| Harmonic Number | Harmonic number to generate the maximum photon intensity at a given photon energy |
| Observer Time | Time in the laboratory frame (for observer) |
| Horizontal Electric Field | Electric field of radiation |
| Vertical Electric Field | |
| Horizontal Real Field | Complex amplitude of radiation evaluated at a given photon energy |
| Horizontal Imaginary Field | |
| Vertical Real Field | |
| Vertical Imaginary Field | |
| Separability | Refer to Separability |
| Deg. Coherence (X) | Refer to Degree of Spatial Coherence |
| Deg. Coherence (Y) | |
| Deg. Coherence (Total) |
Calculation Status/Processes
To configure a number of calculations with different conditions, run [Run]-[Create Process] command every time you finish specifying all the parameters. Then the "Calculation Status/Processes" subpanel appears in the "Main Parameters" panel to show the calculation list currently saved in a temporary memory. Repeat it until all the calculations are specified. Click "Remove" button to delete the selected process, or "Cancel All" to clear out all the processes. Run [Run]-[Start Calculation] command to start the calculation processes, then a progressbar is displayed to show the status of each process.
Scanning a Parameter
Besides the method described above, it is possible to configure a lot of Calculation Status/Processes at once by scanning a specific parameter. To do so, right click the target parameter in one of the subpanels after selecting the Calculation Type, and click [Scan This Parameter] in the context menu. Then specify the configurations for scanning in the dialog box as shown below. Note that the context menu does not pop up for parameters that cannot be used for scanning.
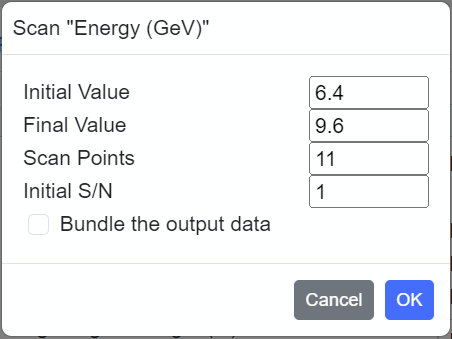
Input the initial & final values, and number of points for scanning. For several parameters to be specified by an integer, scanning interval instead of the number of points should be given. Note that the "Bundle the output data" option is to bundle all the output data into a single output file, which can be retrieved later in the "Post-Processing" panel. The availability of this option depend on the selected Calculation Type.
If the target parameter forms a pair, such as βx, y (horizontal and betatron functions), the user is requested to select the dimension for scanning: [Scan Parameter 1D/2D]. For the 2D scanning, configurations for the both parameters are needed.
After configuration, click "OK" button to create a "Calculation Status/Processes". Then the specified parameters are saved in a temporary memory and the scanning process is saved in the calculation list. Run [Run]-[Start Calculation] command to start the calculation.
Notes on Scanning ε1st
When scanning the fundamental energy of undulators having both (horizontal and vertical) K values (Kx and Ky), such as elliptic undulators, the ratio of the two (Kx/Ky) depends on "Gap-Field Relation" option as summarized below.
| Gap-Field Relation | Details |
| None | Kx/Ky is the same as that currently displayed in the GUI, and is kept constant for different values of ε1st. |
| Automatic | Kx/Ky is determined by "Geometrical Factor (x,y)". |
| Import Table | Kx/Ky is determined by "Gap vs. Field" data imported in Pre-Processing subpanel. |
Parallel Computing
To reduce the computation time, parallel computing based on the MPI is available in SPECTRA. To enable this option, refer to MPI Settings setup dialog.
Advanced Functions
Besides the fundamental properties of SR such as the flux and radiation power, which can be calculated in a rather straightforward manner, SPECTRA offers a method to evaluate a number of special characteristics of SR: Surface Power Density, Volume Power Density, Characterization at the Source Point, Coherent Mode Decomposition. In what follows, details of them are explained.
Surface Power Density
The surface power density is defined as the radiation power per unit surface area of the target object, which should be distinguished from the (normal) power density defined as the power per unit area of the transverse (x,y) plane. If the normal vector of the surface of the target object is parallel to z, there is no difference between the two. This is not the case when the normal vector is perpendicular to z; the surface power density in this configuration is much lower than the normal power density as easily understood.
Computation of the surface power density is usually much more complicated than that of the normal power density. This comes from the fact that the incident angle of SR largely depends on the longitudinal position where it is emitted, if the surface of the target object has a small glancing angle. This is not the case for computing the normal power density, where the incident angle is always nearly 90 degrees.
Volume Power Density
The volume power density is defined as the radiation power absorbed per unit volume in an object illuminated by radiation. In a mathematical form it is given by \[\frac{d^3P(x,y,D)}{dxdydD}=C\int \frac{d^2F(x,y,\omega)}{dxdy}[1-\mbox{e}^{-\mu(\omega)D}]\mu_{en}(\omega)d\omega,\] where $\mu$ & $\mu_{en}$ are the linear attenuation & energy absorption coefficients at the photon energy $\hbar\omega$, $D$ is the distance from the surface of the object ("Depth"), and $C$ is a unit conversion factor. Note that glancing-incidence conditions can be specified as explained in the relevant parameters.
Characterization at the Source Point
In contrast to other calculations in which the observation point is assumed to be located downstream of the light source, characteristics exactly at the source point (center of the light source, z=0) are evaluated in this calculation. This is possible by propagating the emitted radiation backward to the source point using wave optics. Two options are available as follows.
Wigner Function
The photon flux density in the phase space spanned by the spatial $(x,y)=\boldsymbol{r}$ and angular $(x',y')=\boldsymbol{r}'$ coordinates, which is referred to as the phase-space density and denoted by $d(x,y,x',y')$, is an important physical quantity to characterize SR as a light source. Its maximum value, which is known as brilliance or brightness, gives the information of how many coherent photons are available. Its distribution in the phase space is necessary to carry out the ray-trace simulation based on the geometrical optics.
It is worth noting that the angular profile of SR in the far-field region is obtained by integrating $d(x,y,x',y')$ over $(x,y)$, while the spatial profile in the near-field region is obtained by integrating over $(x',y')$. Also note that these spatial and angular profiles can be computed directly from an analytical formulas based on classical electrodynamics. It should be noted, however, that there is no analytical method to calculate $d(x,y,x',y')$ directly from the first principle. The Wigner function $W(x,y,x',y')$ is introduced in SR formulation to solve this problem and makes it possible to compute $d(x,y,x',y')$ from the complex amplitude of radiation.
SPECTRA is equipped with several functions to compute the phase-space density not only for the single electron, but also for more practical conditions, i.e., the electron beam with finite emittance and energy spread. The resultant phase-space density can be computed as a function of various variables: photon energy, K value, and phase-space coordinates. For details of numerical implementation of the Wigner function, refer to [4].
Energy Dependence
The phase-space density is calculated as a function of the photon energy with other conditions being fixed. In the case of undulator radiation, the target harmonic number should be specified as well.
K Dependence
The phase-space density of undulator radiation at a specific harmonic is calculated as a function of the undulator K value. Note that the photon energy should be given as a detuning parameter with respect to the exact harmonic energy. If the calculation is done on-axis (x=y=x'=y'=0), the resultant data are comparable to the brilliance roughly estimated by a Gaussian approximation, but are based on a more rigorous method using the Wigner function.
Phase-Space Distribution
The distribution of the phase-space density is calculated as a function of the phase-space coordinate variables: x, y, x', and y'. Five types of calculation conditions are available as follows.
- X-X' (Sliced): $W(x,y_{fix},x',y_{fix}')$
- X-X' (Projected): $W_x(x,x')$
- Y-Y' (Sliced): $W(x_{fix},y,x_{fix}',y')$
- Y-Y' (Projected): $W_y(y,y')$
- X-X-Y-Y' : $W(x,y,x',y')$
where $W_x$ is defined as \[W_x=\int\!\!\!\!\int W(x,x',y,y')dydy',\] and a similar expression for $W_y$.
Related Characteristics
When the 4D phase-space density is calculated, two important properties related to the Wigner function method are available: separability and total degree of spatial coherence. The details of them are explained as follows.
| Property | Details |
| Separability | In most cases, especially when the electron beam emittance is not too small compared to the optical emittance at the target wavelength, the phase-space density and thus the Wigner function can be separated into two functions $W_x$ and $W_y$. Namely, the Wigner function $W$ can be substituted for by $W_d = W_xW_y/F$, where $F$ is the total photon flux, and the numerical cost for evaluation of the phase-space density is significantly reduced. To evaluate the consistency between the two functions $W$ and $W_d$ and to examine if the above discussions are valid under a specific condition, the separability $\kappa$ has been introduced, which is defined as \[\kappa=1-\sqrt{\frac{\langle(W_d-W)\rangle^2}{\langle W^2\rangle}},\] where $\langle f\rangle$ denotes the average of the function $f$ over the range of interest. |
| Degree of Spatial Coherence | The degree of spatial coherence $\zeta$ in SPECTRA is defined as \[\zeta=\left(\frac{\lambda}{F}\right)^2\int\!\!\!\!\int W^2(\boldsymbol{r},\boldsymbol{r}')d\boldsymbol{r}\boldsymbol{r}',\] which is actually a spatial average of the degree of spatial coherence $\mu^2(\boldsymbol{r}_1,\boldsymbol{r}_2)$ usually calculated at two different points $\boldsymbol{r}_1$ and $\boldsymbol{r}_2$. This is to avoid the complexity of expressing the function by two coordinate variables. Using the two functions $W_x$ and $W_y$, the degree of spatial coherence in the horizontal or vertical direction can be defined in a similar manner. |
Note that the above properties, $\kappa$, $\zeta$, $\zeta_x$, and $\zeta_y$ are evaluated by a simple summation of quadratic forms of Wigner functions given at a number of grid points specified by the user, and the accuracy of integration is not checked. The user is required to input the range and number of mesh that are sufficiently wide and large to obtain a reliable result. One solution is to first check the profile of the projected Wigner functions in the 2D phase space, then input these parameters.
Spatial Profile
Spatial profile of the photon density, i.e., the spatial flux density is computed at the source point. This may be useful when discussing the profile of the photon beam after focusing optical components in the SR beamline. To be more specific, the spatial profile computed with this scheme reproduces the photon beam profile at the focal point of the unit magnification optical system.
Coherent Mode Decomposition
Coherent Mode Decomposition is a mathematical method to decompose the partially coherent radiation into a number of coherent modes. Because the propagation of each mode can be described by wave optics, designing the optical elements can be much more reliable than that with the conventional ray-tracing that is based on geometrical optics.
Mathematical Form
In the numerical CMD implemented in SPECTRA, the Wigner function $W$ is supposed to be approximated by $W'$ composed of several coherent modes, namely, \[W'=f\sum_{p=0}^{M}\mathscr{W}(\Psi_p,\Psi_p),\] with $\mathscr{W}$ meaning an operator to calculate the Wigner function of the $p$-th order coherent mode, whose complex amplitude is represented by a function $\Psi_p$, and $M$ is the maximum order of the coherent modes. The function $\Psi_p$ is assumed top have a form \[\Psi_p=\sum_{q=0}^{N_p}a_{h,j}\phi_h(\hat{x})\phi_j(\hat{y}),\] with \[\phi_m(\zeta)=\frac{2^{1/4}}{\sqrt{2^m m!}}\mbox{e}^{-\pi\zeta^2}H_m(\sqrt{2\pi}\zeta),\] denoting the m-th order Hermite-Gaussian (HG) function, where $\hat{\boldsymbol{r}=(\hat{x},\hat{y})=(x/\sqrt{\pi}w_x,y/\sqrt{\pi}w_y)}$ is the normalized transverse coordinate, $a_{h,j}$ is the amplitude of the HG function of $\phi_h(\hat{x})\phi_j(\hat{y})$, $H_m$ is the Hermite polynomial of the order $m$, and $N_p$ denotes the maximum order of the HG modes in the p-th coherent mode. Note that the indices $h$ and $j$ are given as a function of the integer $q$ and order $p$. The coefficient $f$ and the dimension of $a_{h,j}$ are chosen arbitrarily as long as the above formulas are satisfied. In SPECTRA, they are determined so that $a_{h,j}$ is dimensionless, and \[\sum_{p=0}^{\infty}\int|\Psi_p|^2d\hat{\boldsymbol{r}}=1\] is satisfied. The purpose of the numerical CMD is to compute the coefficient $a_{h,j}$ so that the resultant Wigner function $W'$ well reproduces the original function $W$. For details of the CMD method in SPECTRA, refer to [5].
How to Do?
To perform the CMD in SPECTRA, follow the steps explained below.
- Preparation of the Wigner Function: Before starting the CMD, the user should compute the Wigner function in the phase space. In addition to the 4D Wigner function $W(x,y,x',y')$, the projected ones ($W_x$ and $W_y$), are also available, in which case 1D modal functions are given in the target direction (horizontal or vertical). The range and number of points to calculate the Wigner function should be reasonably wide and large. Note that the JSON format should be chosen as the format of the output file.
- Load the Wigner Function: Open the JSON output file for the Winger function data generated in the above step, by running [File]-[Load Output File]-[Wigner Function for CMD] command. If the Wigner function data is successfully loaded, [CMD with the Wigner Function] menu is enabled under the [Select Calculation]-[Coherent Mode Decomposition] menu. Run it to show configurations for the CMD.
- Arrange the Parameters: In the Configurations subpanel, edit the parameters and options related to the CMD; refer to CMD Parameters for details. After configuration, run [Run]-[Start Calculation] command to start the CMD process.
- Verify the Result: The results of the CMD, such as the modal amplitude $a_{h,j}$, maximum orders of the HG functions, and numerical errors in the CMD process, are save in the output file, which can be directly verified by opening the output file in any text editor.
- Visualization: other data sets specified in the options before starting the CMD, such as the modal profiles and reconstructed Wigner functions, are saved as well, which can be visualized in the "Post-Processing" panel.
Wavefront Propagation
Wavefront Propagation is a function to describe the propagation of synchrotron radiation using the Wigner function. In contrast to the conventional wavefront propagation based on the multi-electron or CMD scheme, it has a potential to complete the computation with a much shorter time. The basic concept has been proposed in 1980's and is found in [10]. Besides simple porpagation in the drift space, two typical optical elements are available: single/double slit and ideal lens. Although the availability is currently limited, efforts are under way to extend the capability of this scheme to a wider variety of components.
How to Do?
To perform the wavefront propagation, follow the steps explained below.
- Prepare and Load the Wigner Function: before starting, the Wigner function data should be generated and loaded. Refer to file:///T:/SourceCode11/spectra/12.0/prj/src/spectra.html#How%20to%20Do? for details.
- Arrange the Parameters: In the Configurations subpanel, edit the parameters and options related to the wavefront propagation; refer to Wavefront Propagation Parameters for details. After configuration, run [Run]-[Start Calculation] command to start the wavefront propagation process.
- Verify the Result: The results of the CMD, such as the modal amplitude $a_{h,j}$, maximum orders of the HG functions, and numerical errors in the CMD process, are save in the output file, which can be directly verified by opening the output file in any text editor.
- Visualization: other data sets specified in the options before starting the CMD, such as the modal profiles and reconstructed Wigner functions, are save as well, which can be visualized in the "Post-Processing" panel.
File Format
Besides the operation based on the GUI, SPECTRA (more precisely, the solver) can be utilized to communicate with external codes for the so-called start-to-end simulations. This actually requires the knowledge of the format of the input and output files, which is explained in the followings.
JSON Format
To deal with the many parameters and options, SPECTRA utilizes the JSON (JavaScript Object Notation) format, which is described by a number of "objects". The object contains a number of "pairs" formed by a "key" and "value", separated by a colon ":", and should be enclosed by a curly bracket {}. The value can be one of the followings: number, array, string and (another) object. An example of the SPECTRA input file is as follows.
{
"Accelerator": {
"Energy (GeV)": 8,
"Current (mA)": 100,
....
"Options": {
"Zero Emittance": false,
"Zero Energy Spread": false
}
},
"Light Source": {
"B (T)": 0.33467954834861074,
"λu (mm)": 32,
....
},
"Configurations": {
"Distance from the Source (m)": 30,
....
},
"Output File": {
"Comment": "",
....
}
}In this example, four JSON objects are found, whose keys are "Accelerator", "Light Source", "Configurations", and "Output File". The value of each object is also an object, which actually specifies the parameters and options, such as "Energy (GeV)": 8, denoting the energy of the electron beam to be 8 GeV.
For details of the JSON format, please refer to any document available online or found in the text.
Input Format
The input file to be loaded by the solver should have 4 JSON objects: "Accelerator", "Light Source", "Configurations", and"Output File". Details of each object are summarized below, where "GUI Notation" is the parameter name displayed in the "Main Parameters" GUI panel, "Key" is the name of the key to be used in the input file, "Format" is the format of the value, and "Default" is the default value. Note that the key name can be either of the "Full" or "Simplified" expression.
Accelerator Object
| GUI Notation | Key | Format | Default | |
| Full | Simplified | |||
| Type | Type | type | Select from: "Storage Ring" "Linear Accelerator" |
Storage Ring |
| Energy (GeV) | Energy (GeV) | eGeV | number | 8 |
| Current (mA) | Current (mA) | imA | number | 100 |
| Bunches | Bunches | bunches | integer | 203 |
| Pulses/sec | Pulses/sec | pulsepps | integer | 60 |
| σz (mm) | σ<sub>z</sub> (mm) | bunchlength | number | 3.9 |
| Bunch Charge (nC) | Bunch Charge (nC) | bunchcharge | number | 0.1 |
| Nat. Emittance (m.rad) | Nat. Emittance (m.rad) | emitt | number | 2.4e-9 |
| Coupling Constant | Coupling Constant | coupl | number | 0.002 |
| Energy Spread | Energy Spread | espread | number | 0.0011 |
| βx,y (m) | β<sub>x,y</sub> (m) | beta | array | [31.2, 5] |
| αx,y | α<sub>x,y</sub> | alpha | array | [0, 0] |
| ηx,y (m) | η<sub>x,y</sub> (m) | eta | array | [0.146, 0] |
| η'x,y | η'<sub>x,y</sub> | etap | array | [0, 0] |
| Bunch Profile | Bunch Profile | bunchtype | Select from: "Gaussian" "[object Object]" |
Gaussian |
| Particle Distribution | Particle Distribution | bunchdata | file name | |
| Current Profile | Current Profile | currdata | object | |
| E-t Profile | E-t Profile | Etdata | object | |
| Injection Condition | Injection Condition | injectionebm | Select from: "Automatic" "Align at Entrance" "Align at Center" "Align at Exit" "Custom" |
Automatic |
| x,y (mm) | x,y (mm) | xy | array | [0, 0] |
| x',y' (mrad) | x',y' (mrad) | xyp | array | [0, 0] |
| Zero Emittance | Zero Emittance | zeroemitt | boolean | false |
| Zero Energy Spread | Zero Energy Spread | zerosprd | boolean | false |
| Single Electron | Single Electron | singlee | boolean | false |
| Additional R56 (m) | Additional R<sub>56</sub> (m) | R56add | number | 0 |
Light Source Object
| GUI Notation | Key | Format | Default | |
| Full | Simplified | |||
| Type | Type | type | Select from: "Linear Undulator" "Vertical Undulator" "Helical Undulator" "Elliptic Undulator" "Figure-8 Undulator" "Vertical Figure-8 Undulator" "Multi-Harmonic Undulator" "Bending Magnet" "Wiggler" "EMPW" "Wavelength Shifter" "Field Mapping" "Periodic: User Defined" "User Defined" |
Linear Undulator |
| Field Profile | Field Profile | fvsz | object | |
| Field Profile (1 Period) | Field Profile (1 Period) | fvsz1per | object | |
| Gap (mm) | Gap (mm) | gap | number | 8 |
| Bx,y (T) | B<sub>x,y</sub> (T) | bxy | array | [0.5, 0.5] |
| B (T) | B (T) | b | number | 0.679498 |
| Main Field (T) | Main Field (T) | bmain | number | 1 |
| Sub Field (T) | Sub Field (T) | subpoleb | number | 1 |
| λu (mm) | λ<sub>u</sub> (mm) | lu | number | 32 |
| Device Length (m) | Device Length (m) | devlength | number | 4.564 |
| # of Reg. Periods | # of Reg. Periods | periods | number | 10 |
| K0x,0y | K<sub>0x,0y</sub> | Kxy0 | array | [0.6, 1] |
| Phase Shift (mm) | Phase Shift (mm) | phase | number | 0 |
| Kx,y | K<sub>x,y</sub> | Kxy | array | [1, 1] |
| K value | K value | K | number | 1 |
| ε1st (eV) | ε<sub>1st</sub> (eV) | e1st | number | 12000 |
| λ1st (nm) | λ<sub>1st</sub> (nm) | lambda1 | number | 1 |
| Harmonic Component | Harmonic Component | multiharm | array | [] |
| ρ (m) | ρ (m) | radius | number | 39.2718 |
| BM Length (m) | BM Length (m) | bendlength | number | 2.8 |
| BM Fringe Length (m) | BM Fringe Length (m) | fringelen | number | 0.05 |
| Main Length (m) | Main Length (m) | mplength | number | 0.1 |
| Sub Length (m) | Sub Length (m) | subpolel | number | 0.05 |
| BM Interval (m) | BM Interval (m) | bminterv | number | 5 |
| Origin for CSR (m) | Origin for CSR (m) | csrorg | number | 0 |
| Field Mapping Data | Field Mapping Data | fmap | file name | |
| Gap-Field Relation | Gap-Field Relation | gaplink | Select from: "None" "Automatic" "Import Table" |
None |
| Br (T) | B<sub>r</sub> (T) | br | number | 1.2 |
| Geometrical Factor (x,y) | Geometrical Factor (x,y) | geofactor | array | [0.6, 0.9] |
| Gap vs. Field | Gap vs. Field | gaptbl | object | |
| APPLE Configuration | APPLE Configuration | apple | boolean | false |
| Field Structure | Field Structure | field_str | Select from: "Antisymmetric" "Symmetric" |
Antisymmetric |
| End Correction Magnet | End Correction Magnet | endmag | boolean | true |
| Natural Focusing | Natural Focusing | natfocus | Select from: "None" "Bx" "By" "Both" |
None |
| Field Offset & Taper | Field Offset & Taper | fielderr | boolean | false |
| Offset x,y (T) | Offset x,y (T) | boffset | array | [0, 0] |
| Lin. Taper x,y (/m) | Lin. Taper x,y (/m) | ltaper | array | [0, 0] |
| Quad. Taper x,y (/m2) | Quad. Taper x,y (/m<sup>2</sup>) | qtaper | array | [0, 0] |
| Add Phase Error | Add Phase Error | phaseerr | boolean | false |
| Random Number Seed | Random Number Seed | seed | integer | 1 |
| σB (%) | σ<sub>B</sub> (%) | fsigma | number | 0.5 |
| σφ (deg.) | σ<sub>φ</sub> (deg.) | psigma | number | 5 |
| σx,y (mm); | σ<sub>x,y</sub> (mm); | xysigma | array | [0.001, 0.001] |
| Tandem Arrangement | Tandem Arrangement | bmtandem | boolean | false |
| Segmentation | Segmentation | segment_type | Select from: "None" "Identical" "2nd: Swap Bx,y" "2nd: Flip Bx" "2nd: Flip By" |
None |
| Number of Segments | Number of Segments | segments | integer | 2 |
| Half Number of Segments | Half Number of Segments | hsegments | integer | 1 |
| Segment Interval (m) | Segment Interval (m) | interval | number | 5 |
| Δφ (π) | Δφ (π) | phi0 | number | 1 |
| Δφ1,2 (π) | Δφ<sub>1,2</sub> (π) | phi12 | array | [0.5, 1.5] |
| Matching Distance (m) | Matching Distance (m) | mdist | number | 5 |
| Periodic β Function | Periodic β Function | perlattice | boolean | false |
Configurations Object
| GUI Notation | Key | Format | Default | |
| Full | Simplified | |||
| Type | Type | type | string | Far Field & Ideal Condition::Energy Dependence::Angular Flux Density |
| Distance from the Source (m) | Distance from the Source (m) | slit_dist | number | 30 |
| Auto Config. for Energy Range | Auto Config. for Energy Range | autoe | boolean | false |
| Harmonic Range | Harmonic Range | hrange | array | [1, 5] |
| Target Harmonic | Target Harmonic | hfix | integer | 1 |
| Maximum Harmonic | Maximum Harmonic | hmax | integer | 5 |
| Detuning | Detuning | detune | number | 0 |
| Energy Range (eV) | Energy Range (eV) | erange | array | [5000, 50000] |
| Energy Pitch (eV) | Energy Pitch (eV) | de | number | 2 |
| Energy Pitch for Integration (eV) | Energy Pitch for Integration (eV) | epitch | number | 2 |
| Points (Energy) | Points (Energy) | emesh | integer | 101 |
| Normalized Energy | Normalized Energy | nefix | number | 1 |
| Target Energy (eV) | Target Energy (eV) | efix | number | 12661 |
| Position x,y (mm) | Position x,y (mm) | xyfix | array | [0, 0] |
| Angle θx,y (mrad) | Angle θ<sub>x,y</sub> (mrad) | qxyfix | array | [0, 0] |
| Surface Pos. x (mm) | Surface Pos. x (mm) | spdxfix | number | 10 |
| Surface Pos. y (mm) | Surface Pos. y (mm) | spdyfix | number | 3 |
| Surface Radius (mm) | Surface Radius (mm) | spdrfix | number | 3 |
| Θ (deg.) | Θ (deg.) | Qnorm | number | 90 |
| Φ (deg.) | Φ (deg.) | Phinorm | number | 90 |
| Glancing Angle (deg.) | Glancing Angle (deg.) | Qgl | number | 90 |
| Azimuth of Incidence (deg.) | Azimuth of Incidence (deg.) | Phiinc | number | 90 |
| Slit Pos.: x,y (mm) | Slit Pos.: x,y (mm) | slitpos | array | [0, 0] |
| Slit Pos.: θx,y (mrad) | Slit Pos.: θ<sub>x,y</sub> (mrad) | qslitpos | array | [0, 0] |
| Δ/Σs: x,y | Δ/Σ<sub>s</sub>: x,y | nslitapt | array | [4, 4] |
| Δx,Δy (mm) | Δx,Δy (mm) | slitapt | array | [2, 1] |
| Δθx,y (mrad) | Δθ<sub>x,y</sub> (mrad) | qslitapt | array | [0.06, 0.03] |
| Slit r1,2 (mm) | Slit r<sub>1,2</sub> (mm) | slitr | array | [0, 1] |
| Slit θ1,2 (mrad) | Slit θ<sub>1,2</sub> (mrad) | slitq | array | [0, 0.03] |
| Power Upper Limit (kW) | Power Upper Limit (kW) | pplimit | number | 0.3 |
| z range (m) | z range (m) | zrange | array | [5, 6] |
| Points (z) | Points (z) | zmesh | integer | 21 |
| Auto Config. for Transverse Range | Auto Config. for Transverse Range | autot | boolean | false |
| Transverse Grid | Transverse Grid | gridspec | Select from: "Automatic" "Normalized" "Fixed" |
Automatic |
| Finer Spatial Grid | Finer Spatial Grid | grlevel | integer | 0 |
| x Range (mm) | x Range (mm) | xrange | array | [-1, 1] |
| θx Range (mrad) | θ<sub>x</sub> Range (mrad) | qxrange | array | [-0.03, 0.03] |
| x Range/Σ | x Range/Σ | wnxrange | array | [-4, 4] |
| Points (x) | Points (x) | xmesh | integer | 41 |
| δx Range (mm) | δx Range (mm) | wdxrange | array | [-0.1, 0.1] |
| δx Range/Σ | δx Range/Σ | wndxrange | array | [-0.1, 0.1] |
| Points (δx) | Points (δx) | wdxmesh | number | 51 |
| y Range (mm) | y Range (mm) | yrange | array | [-0.5, 0.5] |
| θy Range (mrad) | θ<sub>y</sub> Range (mrad) | qyrange | array | [-0.02, 0.02] |
| y Range/Σ | y Range/Σ | wnyrange | array | [-4, 4] |
| Points (y) | Points (y) | ymesh | integer | 41 |
| δy Range (mm) | δy Range (mm) | wdyrange | array | [-0.1, 0.1] |
| δy Range/Σ | δy Range/Σ | wndyrange | array | [-0.1, 0.1] |
| Points (δy) | Points (δy) | wdymesh | number | 51 |
| r Range (mm) | r Range (mm) | rrange | array | [0, 1] |
| θ Range (mrad) | θ Range (mrad) | qrange | array | [0, 0.03] |
| Points (r) | Points (r) | rphimesh | integer | 41 |
| Points (θ) | Points (θ) | qphimesh | integer | 41 |
| φ Range (deg.) | φ Range (deg.) | phirange | array | [0, 90] |
| Points (φ) | Points (φ) | phimesh | integer | 41 |
| Depth Range (mm) | Depth Range (mm) | drange | array | [0, 1] |
| Points (Depth) | Points (Depth) | dmesh | integer | 41 |
| Optical Element | Optical Element | optics | Select from: "None" "Single Slit" "Double Slit" "Ideal Thin Lens" |
None |
| Position (m) | Position (m) | optpos | number | 25 |
| Aperture x (mm) | Aperture x (mm) | aptx | number | 0.2 |
| Slit Distance x (mm) | Slit Distance x (mm) | aptdistx | number | 0.4 |
| Aperture y (mm) | Aperture y (mm) | apty | number | 0.1 |
| Slit Distance y (mm) | Slit Distance y (mm) | aptdisty | number | 0.2 |
| Soft Edge Fringe Size (mm) | Soft Edge Fringe Size (mm) | softedge | number | 0.001 |
| Limit of Diffraction Effect | Limit of Diffraction Effect | diflim | number | 0.02 |
| Larger Angular Range | Larger Angular Range | anglelevel | integer | 0 |
| Focal Length x (m) | Focal Length x (m) | foclenx | number | 10 |
| Focal Length y (m) | Focal Length y (m) | focleny | number | 10 |
| Angular Profile | Angular Profile | aprofile | boolean | false |
| Wigner Function | Wigner Function | wigner | boolean | false |
| Cross Spectral Density | Cross Spectral Density | csd | boolean | false |
| Degree of Coherence | Degree of Coherence | degcoh | boolean | false |
| K Range | K Range | krange | array | [0, 2.3] |
| K⊥ Range | K<sub>⊥</sub> Range | ckrange | array | [0, 5] |
| Points (K) | Points (K) | kmesh | integer | 51 |
| Temporal Range (fs) | Temporal Range (fs) | trange | array | [-0.05, 0.05] |
| Points (Temporal) | Points (Temporal) | tmesh | integer | 10001 |
| γΔθx,y | γΔθ<sub>x,y</sub> | gtacc | array | [1, 1] |
| X' Acceptance (mrad) | X' Acceptance (mrad) | horizacc | number | 0.1 |
| Slice X (mm) | Slice X (mm) | Xfix | number | 0 |
| Slice Y (mm) | Slice Y (mm) | Yfix | number | 0 |
| Slice X' (mrad) | Slice X' (mrad) | Xpfix | number | 0 |
| Slice Y' (mrad) | Slice Y' (mrad) | Ypfix | number | 0 |
| X Range (mm) | X Range (mm) | Xrange | array | [-1, 1] |
| Points (X) | Points (X) | Xmesh | integer | 51 |
| X' Range (mrad) | X' Range (mrad) | Xprange | array | [-0.05, 0.05] |
| Points (X') | Points (X') | Xpmesh | integer | 41 |
| Y Range (mm) | Y Range (mm) | Yrange | array | [-0.04, 0.04] |
| Points (Y) | Points (Y) | Ymesh | integer | 51 |
| Y' Range (mrad) | Y' Range (mrad) | Yprange | array | [-0.02, 0.02] |
| Points (Y') | Points (Y') | Ypmesh | integer | 41 |
| Filtering | Filtering | filter | Select from: "None" "Generic Filter" "BPF: Gaussian" "BPF: Boxcar" "Custom" |
None |
| Filters | Filters | fmateri | array | [] |
| Custom Filter | Custom Filter | fcustom | object | |
| Central Energy (eV) | Central Energy (eV) | bpfcenter | number | 10000 |
| Width (eV) | Width (eV) | bpfwidth | number | 100 |
| Width (σ, eV) | Width (σ, eV) | bpfsigma | number | 100 |
| Max. Trans. Rate | Max. Trans. Rate | bpfmaxeff | number | 1 |
| Absorbers | Absorbers | amateri | array | [] |
| Depth Step | Depth Step | dstep | Select from: "Linear" "Logarithmic" "Export at Arbitrary Positions" |
Linear |
| Depth-Position Data | Depth-Position Data | depthdata | object | |
| Define Obs. Point in | Define Obs. Point in | defobs | Select from: "Position" "Angle" |
Position |
| Normalize Photon Energy | Normalize Photon Energy | normenergy | boolean | false |
| Energy Step | Energy Step | estep | Select from: "Linear" "Logarithmic" |
Linear |
| Slit Aperture Size | Slit Aperture Size | aperture | Select from: "Fixed" "Normalized" |
Fixed |
| Set Upper Limit on Power | Set Upper Limit on Power | powlimit | boolean | false |
| Optimize ΔX' for Computation | Optimize ΔX' for Computation | optDx | boolean | true |
| Level of Smoothing Along X | Level of Smoothing Along X | xsmooth | number | 1 |
| Observation in the Fourier Plane | Observation in the Fourier Plane | fouriep | boolean | false |
| Wiggler Approximation | Wiggler Approximation | wiggapprox | boolean | false |
| Spectral Smoothing | Spectral Smoothing | esmooth | boolean | false |
| Smoothing Window (%) | Smoothing Window (%) | smoothwin | integer | 1 |
| Accuracy Level | Accuracy Level | acclevel | number | 0 |
| Accuracy | Accuracy | accuracy | Select from: "Default" "Custom" |
Default |
| Perform CMD? | Perform CMD? | CMD | boolean | false |
| Apply GS Model | Apply GS Model | GSModel | boolean | false |
| GS Model X/Y | GS Model X/Y | GSModelXY | Select from: "None" "X" "Y" "Both" |
None |
| Export Field Profile | Export Field Profile | CMDfld | Select from: "None" "JSON" "BINARY" "Both" |
None |
| Export Intensity Profile | Export Intensity Profile | CMDint | boolean | false |
| Range: X,Y (mm) | Range: X,Y (mm) | fieldrangexy | array | [1, 0.2] |
| Range: X (mm) | Range: X (mm) | fieldrangex | number | 1 |
| Range: Y (mm) | Range: Y (mm) | fieldrangey | number | 0.2 |
| Step: X,Y (mm) | Step: X,Y (mm) | fieldgridxy | array | [0.005, 0.002] |
| Step: X (mm) | Step: X (mm) | fieldgridx | number | 0.005 |
| Step: Y (mm) | Step: Y (mm) | fieldgridy | number | 0.002 |
| HG Order Limit (X,Y) | HG Order Limit (X,Y) | HGorderxy | array | [50, 50] |
| HG Order Limit (X) | HG Order Limit (X) | HGorderx | number | 50 |
| HG Order Limit (Y) | HG Order Limit (Y) | HGordery | number | 50 |
| Max. HG Order (X,Y) | Max. HG Order (X,Y) | maxHGorderxy | array | [50, 50] |
| Max. HG Order (X) | Max. HG Order (X) | maxHGorderx | number | 50 |
| Max. HG Order (Y) | Max. HG Order (Y) | maxHGordery | number | 50 |
| Maximum CMD Order | Maximum CMD Order | maxmode | number | 100 |
| Flux Cutoff | Flux Cutoff | fcutoff | number | 0.001 |
| Amplitude Cutoff | Amplitude Cutoff | cutoff | number | 0.0001 |
| Compare Wigner Function | Compare Wigner Function | CMDcmp | boolean | false |
| Compare Intensity Profile | Compare Intensity Profile | CMDcmpint | boolean | false |
| FEL Mode | FEL Mode | fel | Select from: "None" "Prebunched FEL" "Seeded FEL" "Seeded with Chirped Pulse" "Seeded with Double Pulse" "Seeded width Custom Pulse" "Reuse Bunch Factor" |
None |
| Seed Spectrum | Seed Spectrum | seedspec | object | |
| Pulse Energy (mJ) | Pulse Energy (mJ) | pulseE | number | 0.1 |
| Wavelength (nm) | Wavelength (nm) | wavelen | number | 267 |
| Pulse Length (FWHM, fs) | Pulse Length (FWHM, fs) | pulselen | number | 40 |
| TL. Pulse Length (FWHM, fs) | TL. Pulse Length (FWHM, fs) | tlpulselen | number | 40 |
| Source Size (FWHM, mm) | Source Size (FWHM, mm) | srcsize | number | 1 |
| Waist Position (m) | Waist Position (m) | waistpos | number | 0 |
| Timing (fs) | Timing (fs) | timing | number | 0 |
| GDD (fs2) | GDD (fs<sup>2</sup>) | gdd | number | 0 |
| TOD (fs3) | TOD (fs<sup>3</sup>) | tod | number | 0 |
| Pulse Energy: 1,2 (mJ) | Pulse Energy: 1,2 (mJ) | pulseE_d | array | [0.1, 0.1] |
| Wavelength: 1,2 (nm) | Wavelength: 1,2 (nm) | wavelen_d | array | [267, 280] |
| TL. Pulse Length: 1,2 (FWHM, fs) | TL. Pulse Length: 1,2 (FWHM, fs) | tlpulselen_d | array | [40, 40] |
| Source Size: 1,2 (FWHM, mm) | Source Size: 1,2 (FWHM, mm) | srcsize_d | array | [1, 1] |
| Waist Position: 1,2 (m) | Waist Position: 1,2 (m) | waistpos_d | array | [0, 0] |
| Timing: 1,2 (fs) | Timing: 1,2 (fs) | timing_d | array | [0, 0] |
| GDD: 1,2 (fs2) | GDD: 1,2 (fs<sup>2</sup>) | gdd_d | array | [0, 0] |
| TOD: 1,2 (fs3) | TOD: 1,2 (fs<sup>3</sup>) | tod_d | array | [0, 0] |
| Step: Initial, Interval (m) | Step: Initial, Interval (m) | svstep | array | [-1, 0.1] |
| Substeps for Radiation | Substeps for Radiation | radstep | number | 5 |
| Photon Energy ROI (eV) | Photon Energy ROI (eV) | eproi | array | [1, 120] |
| Number of Particles | Number of Particles | particles | number | 1000000 |
| e- Energy Interval | e- Energy Interval | edevstep | number | 0.0001 |
| R56 (m) | R<sub>56</sub> (m) | R56 | number | 0 |
| Export Intermediate Data | Export Intermediate Data | exportInt | boolean | true |
| Bunch with Dispersion | Bunch with Dispersion | R56Bunch | boolean | false |
| E-t Data | E-t Data | exportEt | boolean | false |
Output File Object
| GUI Notation | Key | Format | Default | |
| Full | Simplified | |||
| Format | Format | format | Select from: "JSON" "ASCII" "Both" |
JSON |
| Folder | Folder | folder | directory name | |
| Prefix | Prefix | prefix | string | Untitled |
| Comment | Comment | comment | string | |
| Serial Number | Serial Number | serial | integer | -1 |
Output Format
If "JSON" or "Both" is chosen as the "Format" option in the Output File subpanel, a JSON format output file is generated after the calculation completes. Besides the visualization in the "Post-Processing" panel, it can be used for further processing with other external codes. To facilitate it, the structure of the output file is explained below. Note that the order index (for example of an array, column, etc.) in the followings is defined as starting from "0", but not from "1".
"Input" Object
All the parameters and options are stored in this object with the same format as the Input Format. If the output file is opened in the GUI (as an input parameter file), these parameters are displayed and can be used again.
"Output" Object
The calculation results are stored in this object.
| Key | Details | Format |
| dimension | Dimension of the calculation data, or the number of independent variables. | number |
| titles | Titles of individual arrays included in the "data" object. | array (1D) |
| units | Units of individual arrays included in the "data" object. | array (1D) |
| details | Additional information of the 3D-array data, which is generated in several calculation types. For example, those with "Target Harmonics" (flux specific to a specific harmonic) result in a number of data, each of which is 2D and corresponds to the harmonic number. | array (1D) |
| data | Main body of the calculation result data. | array (2D or 3D) |
The format of the "data" object (2D array) is as follows.
- 0th ~ (n-1)-th array: independent variables, where n is the dimension. The length of each array corresponds to the number of calculation points. For example, it is defined by "Points (Energy)" parameter for "Energy Dependence" calculations.
- n-th ~ (n+m-1)-th array: calculated items, where m is the number of items. The length of each array corresponds to the product of the lengths of the independent variable arrays.
As an example, let us consider an "Output" object as follows
"Output": {
"dimension": 1,
"titles": ["Energy","Flux Density","GA. Brilliance","PL(s1/s0)","PC(s3/s0)","PL45(s2/s0)"],
"units": ["eV","ph/s/mr^2/0.1%B.W.","ph/s/mm^2/mr^2/0.1%B.W.","","",""],
"data": [
[5000,5005,...,49995,50000],
[4.02638e+14,3.98914e+14,...,6.66718e+16,6.81642e+16],
[3.2776e+16,3.24789e+16,...,6.64598e+18,6.79476e+18],
[0.999949,0.999947,...,0.999703,0.999713],
[0,0,...,0,0],
[-8.67036e-18,-8.97758e-18,...,-1.72714e-17,-1.6893e-17]
]
}The data is composed of 1 independent variable (Energy) and 5 items (Flux Density etc.). The 0th array ([5000,...]) corresponds to the photon energy, and the 1st ([4.02638e+14,...]) to the flux density, etc.
In case the dimension is larger than 1 and thus more than one independent variables exist, the order index j of the item array is given as \[j=j_0+j_1N_0+j_2N_0N_1+\cdots,\] where $j_i$ and $N_i$ refer to the order index and number of data points of the $i$-th variable.
In some case, 3D data array composed of a number of 2D arrays with the same format as above is stored; each of 2D array is characterized by the "details" object. An example is shown below.
"Output": {
"dimension": 1,
"titles": ["Harmonic Energy","Peak Energy","K Value","Gap","Flux Density",...],
"units": ["eV","eV","","","ph/s/mr^2/0.1%B.W.",...],
"details": ["Harmonic: 1","Harmonic: 3","Harmonic: 5"],
"data": [
[
[18977.5,18707.1,...,4702.57,4336.24],
[18927.2,18657.6,...,4692.37,4326.97],
[0.040015,0.174748,...,2.46527,2.6],
[50,35.2675,...,8.58047,8.01609],
[7.24659e+15,1.3423e+17,...,1.90452e+18,1.82972e+18],
[6.91663e+17,1.27995e+19,...,1.5325e+20,1.44896e+20],
[0.999995,0.999995,...,0.999998,0.999998],
[0,0,...,0,0],
[-6.23832e-19,-6.15261e-19,...,-8.10339e-19,-7.90166e-19]
],
[
[56932.5,56121.2,54374,...,14107.7,13008.7],
[47488.9,56019.4,54276.1,...,15312,14087.7,12990.4],
[0.040015,0.174748,...,2.46527,2.6],
[50,35.2675,...,8.58047,8.01609],
[3.235e+10,5.91631e+13,...,1.21888e+18,1.20334e+18],
.....
],
[
[94887.4,93535.3,...,23512.9,21681.2],
[85444.8,84227.3,...,23487.4,21658],
[0.040015,0.174748,...,2.46527,2.6],
[50,35.2675,...,8.58047,8.01609],
[7.1207e+11,1.37382e+13,...,7.22944e+19,7.31154e+19],
.....
]
]
}The "details" object in this example specify the harmonic number, i.e., 1st, 3rd and 5th harmonics, and the maximum flux density near the harmonic energy, and other related characteristics are calculated as a function of the K value, for the three different harmonic numbers. The "data" object is then composed of three 2D arrays and thus forms a 3D array.
Objects Related to CMD
The results of Coherent Mode Decomposition, such as the modal amplitude and profiles, are saved separately from the "data" object described above. The details of them are explained below.
"Coherent Mode Decomposition" Object
| Key | Details | Symbol | Unit |
| maxorder | Maximum order of the Hermite-Gaussian (HG) functions to form the coherent mode | ||
| wavelength | Wavelength of the Wigner function used for CMD | $\lambda$ | m |
| photon flux | Total photon flux evaluated from the Wigner function | $F$ | photons/sec/0.1%b.w. |
| size | Parameters to define the arguments of HG functions | $\sigma$ or $\sigma_{x,y}$ (1D or 2D) | m |
| order | Indices to define the orders of HG functions for a specific coherent mode | ||
| numerical validity |
Validity of the CMD
|
||
| coefficient | Coefficient to retrieve the Wigner function from the modal amplitude | $W_0$ | photons/sec/mm2/mrad2/0.1%b.w. |
| anm.re | Matrix to represent the complex amplitude of HG functions for each coherent mode, real part | ||
| anm.im | Imaginary part of the above matrix |
How to retrieve the flux and Wigner function from the modal amplitue?
The flux density ($I_n$) and Wigner function ($W_n$) of the $n$-th mode can be retrieved form the complex amplitude $a_n$ determined by the CMD according to the following formulas, using the symbols summarized in the above table.
For 1D case (CMD with 2D Wigner function):\[I_n(x)=|a_n(x)|^2\frac{F}{2\sqrt{\pi}\sigma}\times 10^{-3},\] \[W_n(x,\theta_x')=\frac{W_0}{2\sqrt{\pi}\sigma}\int a_n\left(x-\frac{x'}{2}\right)a_n^*\left(x+\frac{x'}{2}\right)\mbox{e}^{ik\theta_x x'}dx',\]
For 2D case (CMD with 4D Wigner function):\[I_n(\boldsymbol{r})=|a_n(\boldsymbol{r})|^2\frac{F}{4\pi\sigma_x\sigma_y}\times 10^{-6},\] \[W_n(\boldsymbol{r},\boldsymbol{\theta})=\frac{W_0}{4\pi\sigma_x\sigma_y}\int a_n\left(\boldsymbol{r}-\frac{\boldsymbol{r}'}{2}\right)a_n^*\left(\boldsymbol{r}+\frac{\boldsymbol{r}'}{2}\right)\mbox{e}^{ik\boldsymbol{\theta}\boldsymbol{r}'}d\boldsymbol{r}',\]
where $k=2\pi/\lambda$ is the wavenumber of radiation.
Other Objects
A number of data sets evaluated by post-processing the CMD results described above are saved as follows. Note that the format of each object is the same as that of the "data" object.
| Object Name | Details |
| Modal Flux | Information about how much flux is contained in each coherent mode. |
| Modal Profile/Modal Intensity | Spatial profile of the complex field amplitude/intensity calculated for each coherent mode. Note that the calculation range and number of points are specified in CMD Parameters. |
| Flux Density Profile | Flux density profile reconstructed from the modal and Wigner functions by projection to the real space (X,Y) |
| Wigner Func. (X,X') | Wigner function reconstructed from the modal profile, to be compared with the original one to check how the CMD was successful. To facilitate the comparison, both functions are projected on the (X,X') phase space. |
| Wigner Func. (Y,Y') | Same as the above, but for the (Y,Y') phase space. |
Objects Related to FEL Mode
When FEL Mode and Export Intermediate Data options are enabled, numerical data generated while solving the FEL equation, such as variation of the electron beam temporal profile and growth of the FEL radiation pulse, are recorded as summarized below.
| Object Name | Details |
| Current Profile | Current profile of the electron beam. |
| E-t Profile | Electron density in the E-t (energy-time) phase space. |
| Current Profile with Dispersion | Current profile of the electron beam after passing through a virtual dispersive section. Available if Bunch with Dispersion option is enabled. |
| E-t Profile with Dispersion | Electron density in the (E-t) phase space after the virtual dispersive section. Available if Bunch with Dispersion option is enabled. |
| Bunch Factor | Bunch factor of the electron beam. |
| Pulse Energy | Total energy of the radiation pulse. |
| On-Axis Field | Waveform of the on-axis electric field of radiation in the far-field zone. |
| Inst. Power | Temporal profile of the instantaneous radiation power. |
| Spectrum | Spectrum of the radiation pulse. |
Standalone Mode
Besides the desktop application as described above, the solver of SPECTRA can be run in a standalone mode. Note that in the followings, [spectra_home] refers to the directory where SPECTRA has been installed.
When [Run]-[Start Calculation] command is executed, the SPECTRA GUI creates an input parameter file ("*.json") and invokes the solver ("spectra_solver" or "spectra_solver_nompi" depending on whether the parallel computing option is enabled or not) located in the same directory as the main GUI program, with the input file as an argument. This means that SPECTRA (solver) can be run without the GUI, if the input file is prepared by an alternative method, and a batch process will be possible. To do so, prepare the input file according to the descriptions in Input Format and run the solver as follows
[spectra_home]/spectra_solver_nompi -f [input file]without parallel computing, or
mpiexec -n 4 [spectra_home]/spectra_solver_nompi -f [input file]with parallel computing (4 processes in this example).
It should be noted that the names of the parameters and options ("key" of the object) should be totally correct, including the units and inserted space characters. In addition, the number of parameters and options actually needed for a specific calculation depend on its condition. To avoid potential errors and complexity in preparing the input file, it is recommended to create a "master input file" specific to the desired calculation type, by running [Run]-[Export as ASCII] command. Then, just modify the values of desired parameters to prepare the input file.
Note that this usage has not been officially supported before ver. 11.0, simply because the input file format was original and difficult to read.
Python User Interface
To support the expanding users of python language, SPECTRA has started official support for python, since ver. 12.0. To make use of this function, python version 3.8 or later is needed, and the user is requested to install a python package spectra-ui (SPECTRA User Interface). Refer to the instructions for details of spectra-ui.
References
- T. Tanaka and H. Kitamura, "SPECTRA - a synchrotron radiation calculation code," J. Synchrotron Radiation 8, 1221 (2001)
- T. Tanaka and H. Kitamura, "Recent Progress of the Synchrotron Radiation Calculation Code SPECTRA", Proc. 9th Int. Conf. Synchrotron Rad. Instrum. (SRI2006), 355
- T. Tanaka, "Major upgrade of the synchrotron radiation calculation code SPECTRA," J. Synchrotron Radiation 28, 1267 (2021)
- T. Tanaka, "Numerical methods for characterization of synchrotron radiation based on the Wigner function method," Phys. Rev. ST-AB 17, 060702 (2014)
- T. Tanaka, "Coherent mode decomposition using mixed Wigner functions of Hermite-Gaussian beams," Optics Letters 42, 1576 (2017)
- R. Walker, "Interference effects in undulator and wiggler radiation sources", Nucl. Instrum. Methods Phys. Res., Sect. A 335, 328 (1993)
- T. Tanaka and H. Kitamura, "Simple scheme for harmonic suppression by undulator segmentation," Journal of Synchrotron Radiation 9, 266 (2002)
- T. Tanaka and H. Kitamura, "Production of linear polarization by segmentation of helical undulator," Nucl. Instrum. Meth. A490, 583 (2002)
- T. Tanaka, "Universal representation of undulator phase errors," Phys. Rev. AB 21, 110704 (2018)
- K. J. Kim, "Characteristics of Synchrotron Radiation," in Physics of Particle Accelerators, AIP Conf. Proc. 184 (Am. Inst. Phys., New York, 1989), p. 565.
Acknowledgements
This software includes the work that is distributed in the Apache License 2.0, and relies on a number of libraries & database as summarized below, which are gratefully appreciated.
- Node.js: Javascript runtime environment to run Javascript code without a web browser (https://nodejs.org/en/).
- tauri: application toolkit to build software for all major desktop operating systems using web technologies. (https://tauri.app/)
- Plotly.js: Javascript graphing library to facilitate data visualization (https://nodejs.org/en/)
- Boost C++: Set of libraries for the C++ language (https://www.boost.org/)
- EIGEN: C++ template library for linear algebra (https://eigen.tuxfamily.org/index.php?title=Main_Page)
- mathjax: Javascript library to display mathematical formulas in HTML documents (https://www.mathjax.org/)
- picojson: JSON parser for C++ language (https://github.com/kazuho/picojson)
- mucal.c: Source code to calculate the x-ray absorption coefficients (http://www.csrri.iit.edu/mucal.html)
- NIST database: Database for the mass energy-absorption coefficients (https://www.nist.gov/pml/x-ray-mass-attenuation-coefficients)
- General Purpose FFT Package (https://www.kurims.kyoto-u.ac.jp/~ooura/fft.html)